I. Description d’un gaz parfait
1. Le modèle du gaz parfait
Un gaz est un ensemble de molécules (ou d’atomes) libres de se déplacer les uns par rapport aux autres. Nous ne nous intéresserons, ici, qu’au mouvement de translations de ces particules laissant de coté la rotation et la vibration de celles-ci. Un gaz parfait est défini par les hypothèses suivantes : - Un gaz parfait est un ensemble de particules ponctuelles et sans interaction entre elles en dehors des chocs. - Les molécules du gaz sont réparties de manière homogène dans tout l’espace qui leur est offert. De ce fait si N est le nombre de particules du gaz et V le volume de celui-ci, on peut définir la densité moléculaire par .
- Toutes les molécules du gaz n’ont pas la même vitesse, il existe une répartition statistique de ces vitesses (gauss). Cette répartition des vitesses est stationnaire et indépendante des coordonnées de la particule.
- Toutes les directions de l’espace sont équiprobables pour le vecteur vitesse, on dit que la répartition du vecteur vitesse est isotrope.
.
- Toutes les molécules du gaz n’ont pas la même vitesse, il existe une répartition statistique de ces vitesses (gauss). Cette répartition des vitesses est stationnaire et indépendante des coordonnées de la particule.
- Toutes les directions de l’espace sont équiprobables pour le vecteur vitesse, on dit que la répartition du vecteur vitesse est isotrope.
2. Calcul de la pression
On se propose, à partir des hypothèses précédentes, de calculer la force qu’un gaz parfait exerce sur un élément de paroi orienté vers la normale extérieure.
Cette force est due aux chocs des molécules sur cette paroi. Deux phénomènes interviennent alors :
- l’absorption d’une molécule par la paroi. La paroi reçoit alors de la molécule une certaine quantité de mouvement
orienté vers la normale extérieure.
Cette force est due aux chocs des molécules sur cette paroi. Deux phénomènes interviennent alors :
- l’absorption d’une molécule par la paroi. La paroi reçoit alors de la molécule une certaine quantité de mouvement 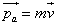 .
- La désorption, les molécules ne restent pas collées à la paroi, elles s’en retournent vers le gaz et emportent avec elles une quantité de mouvement
.
- La désorption, les molécules ne restent pas collées à la paroi, elles s’en retournent vers le gaz et emportent avec elles une quantité de mouvement  Finalement le gaz échange avec la paroi la quantité de mouvement :
Finalement le gaz échange avec la paroi la quantité de mouvement :


 la quantité de mouvement due à l’absorption durant dt
-
la quantité de mouvement due à l’absorption durant dt
-  la quantité de mouvement due à la désorption durant dt
la quantité de mouvement due à la désorption durant dt
Calcul de 

Figure 1
 sont celles qui sont contenues dans le cylindre de base dS et de longueur vdt.
sont celles qui sont contenues dans le cylindre de base dS et de longueur vdt.

Figure 2

 le nombre d’atome par unité de volume ayant un vecteur vitesse
le nombre d’atome par unité de volume ayant un vecteur vitesse 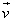 , le nombre de particules de vitesse
, le nombre de particules de vitesse  atteignant la paroi durant dt est :
atteignant la paroi durant dt est :

 est alors :
est alors :




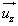 pourront atteindre la paroi. On note
pourront atteindre la paroi. On note  le nombre de particules satisfaisant à cette condition par unité de volume.
Il est temps maintenant d’utiliser une hypothèse du gaz parfait : l’isotropie des vitesses. Puisque toutes les directions sont équiprobable, la probabilité de trouver une particule se dirigeant vers
le nombre de particules satisfaisant à cette condition par unité de volume.
Il est temps maintenant d’utiliser une hypothèse du gaz parfait : l’isotropie des vitesses. Puisque toutes les directions sont équiprobable, la probabilité de trouver une particule se dirigeant vers  est la même que celle de trouver une particule se dirigeant vers
est la même que celle de trouver une particule se dirigeant vers 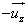 , on en déduit alors :
, on en déduit alors :

 du fait de l’absorption des particules s’écrit :
du fait de l’absorption des particules s’écrit :

Calcul de 
 , chaque particule emporte donc la quantité de mouvement
, chaque particule emporte donc la quantité de mouvement  .
Les particules de vitesse v’ qui ont quitté la paroi durant un temps dt se trouve forcément dans le cylindre de base dS et hauteur
.
Les particules de vitesse v’ qui ont quitté la paroi durant un temps dt se trouve forcément dans le cylindre de base dS et hauteur  et possèdent un vecteur vitesse dirigé vers
et possèdent un vecteur vitesse dirigé vers 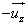 . On en déduit :
. On en déduit :


 du fait de la désorption est :
du fait de la désorption est :


Calcul de 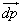




 qu’une particule ayant un vecteur vitesse de composantes
qu’une particule ayant un vecteur vitesse de composantes  , de ce fait, la moyenne
, de ce fait, la moyenne 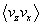 est nulle. Il en va de même pour
est nulle. Il en va de même pour  . La quantité de mouvement échangée par le gaz n’a de composante que suivant la normale à la surface.
L’isotropie des vitesses permet aussi d’écrire :
. La quantité de mouvement échangée par le gaz n’a de composante que suivant la normale à la surface.
L’isotropie des vitesses permet aussi d’écrire :






Calcul de la pression d’un gaz parfait
En utilisant la relation fondamentale de la dynamique, on obtient :

 (1)
(1)
3. Définition de la température d’un Gaz Parfait
La température d’un gaz parfait évalue l’énergie cinétique moyenne des particules de ce gaz. Elle est définie par la thermodynamique statistique qui aboutit à la relation suivante : (2)
(2)
 est la constante de Boltzmann et vaut 1,38.10-23 J.K-1
- T est appelée température cinétique du GP, elle s’exprime en kelvin.
est la constante de Boltzmann et vaut 1,38.10-23 J.K-1
- T est appelée température cinétique du GP, elle s’exprime en kelvin.
4. Equation d’état
On peut établir, à partir des éléments précédents, l’équation d’état du gaz parfait. La vitesse quadratique moyenne des particule n’est pas une grandeur très pratique, de ce fait il serait judicieux de « l’effacer » de la fonction d’état. Reprenons pour cela la définition (2) de la température du GP, on peut en retirer l’expression de la vitesse quadratique moyenne : (3)
(3)



 . Et on obtient finalement :
. Et on obtient finalement :

5. Energie interne
L’énergie interne d’un gaz parfait correspond à l’énergie de translation de chacune des particules(si on fait abstraction de la rotation et de la vibration), autrement dit, l’énergie interne d’un gaz parfait est la somme des énergies cinétiques de chaque particule du gaz :






6. Capacités calorifiques du gaz parfait
Nous avons montré précédemment que la capacité calorifique à volume constant d’un corps s’écrit :
 . Cette valeur a été obtenue en ne considérant que le mouvement de translation du gaz, mais il existe aussi deux autres mouvements propres aux molécules du gaz dont nous n’avons pas tenu compte :
- la rotation
- la vibration
Chacun de ces mouvements est susceptible d’augmenter l’énergie interne du gaz parfait, la question est de savoir dans quelles proportions. Nous allons y répondre de la manière assez simple, mais pour cela il nous faut définir un degré de liberté de la molécule. Un degré de liberté représente la possibilité pour la molécule d’effectuer un mouvement.
On postule maintenant qu’à chaque degré de liberté de la molécule de gaz parfait, on associe la même quantité d’énergie. Il existe trois directions de translation, donc trois degré de liberté dans le calcul que nous avons effectué au paragraphe précédent, on associe donc à chacun d’entre eux l’énergie interne
. Cette valeur a été obtenue en ne considérant que le mouvement de translation du gaz, mais il existe aussi deux autres mouvements propres aux molécules du gaz dont nous n’avons pas tenu compte :
- la rotation
- la vibration
Chacun de ces mouvements est susceptible d’augmenter l’énergie interne du gaz parfait, la question est de savoir dans quelles proportions. Nous allons y répondre de la manière assez simple, mais pour cela il nous faut définir un degré de liberté de la molécule. Un degré de liberté représente la possibilité pour la molécule d’effectuer un mouvement.
On postule maintenant qu’à chaque degré de liberté de la molécule de gaz parfait, on associe la même quantité d’énergie. Il existe trois directions de translation, donc trois degré de liberté dans le calcul que nous avons effectué au paragraphe précédent, on associe donc à chacun d’entre eux l’énergie interne  . Si on rajoute maintenant les deux degrés de libertés (rotation et vibration), l’énergie interne d’une mole de gaz parfait est alors :
. Si on rajoute maintenant les deux degrés de libertés (rotation et vibration), l’énergie interne d’une mole de gaz parfait est alors :







7. Propriétés thermoélastiques des gaz
Pour décrire le comportement des fluides à diverses transformations, on introduit les coefficients thermoélastiques : - le coefficient de dilatation à pression constante, très utilisé en thermométrie




 On remarque, via l’expression de
On remarque, via l’expression de  que la compressibilité d’un gaz parfait est grande devant celle des phases condensées en particulier.
que la compressibilité d’un gaz parfait est grande devant celle des phases condensées en particulier.
II. Mélange de gaz parfaits
1. Expérience de Berthollet
Deux récipients communiquent par un robinet et contiennent respectivement de l’hydrogène (haut) et du gaz carbonique (bas) dans les mêmes conditions de température et de pression ; la pression de chacun des compartiments est indiquée par un manomètre à huile.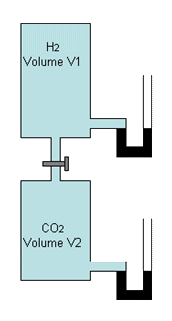
Figure 3

 . L’idéalité de deux gaz n’assure pas l’idéalité de leur mélange.
Un mélange est dit idéal si les interactions entre les particules sont les même avant et après le mélange, autrement dit, les différents constituants du mélange ne se « voient » pas.
. L’idéalité de deux gaz n’assure pas l’idéalité de leur mélange.
Un mélange est dit idéal si les interactions entre les particules sont les même avant et après le mélange, autrement dit, les différents constituants du mélange ne se « voient » pas.
2. Pression partielle
On appelle pression partielle d’un gaz dans un mélange, la pression qu’il exercerait s’il était seul. Soient V1 et V2 les volumes des récipients et P la pression totale. On peut calculer les pressions partielles de chacun des gaz dans l’expérience précédente en utilisant la loi de Mariotte. La température étant constante, le produit PV reste constant et on peut écrire : - pour l’hydrogène


3. Fraction molaire
Soit un mélange idéal de r gaz parfaits, désignons par ni le nombre de moles du constituant n°i et par Pi sa pression partielle, on note P la pression totale. On appelle fraction molaire du gaz n°i dans le mélange la quantité :

III. Le gaz réel
1. Forces intermoléculaires
Le modèle du gaz parfait suppose qu’il n’existe aucune interaction entre les molécules en dehors des chocs. En réalité, il existe forces intermoléculaires plus connues sous le nom de forces de Van der Waals. Ces forces résultent des propriétés électriques des molécules. Nous verrons dans le cours d’électrostatique que les forces de Van der Waals sont dues à l’interaction entre les moments dipolaires des molécules. Pour l’heure, nous allons nous contenter d’une description qualitative qui va nous amener à modifier l’équation d’état des gaz parfaits. L’énergie potentielle d’interaction entre les molécules a l’allure indiquée sur la figure 4.
Figure 4
2. Equation de Van Der Waals
Le constat précédent va nous permettre de proposer une modification de l’équation d’état des gaz parfaits. Intéressons nous au terme de pression. Nous avons réalisé le calcul de la pression d’un gaz parfait, cette pression est le résultat des chocs successifs des molécules sur la paroi. Dans le gaz parfait, rien ne retient les molécules à l’intérieur du gaz, dans le gaz réel des forces attractives tendent à retenir les molécules au sein de leurs consœurs et de ce fait les chocs avec la paroi sont moins violents (ou moins nombreux). La figure illustre ce propos.
Figure 5
 où
où  est la pression terme.
D’autre part les molécules de gaz réel ne sont pas ponctuelles, le volume qui leur est offert n’est donc pas le volume V de l’enceinte mais un volume plus faible, il faudra donc remplacer le terme V dans l’équation des gaz parfaits par
est la pression terme.
D’autre part les molécules de gaz réel ne sont pas ponctuelles, le volume qui leur est offert n’est donc pas le volume V de l’enceinte mais un volume plus faible, il faudra donc remplacer le terme V dans l’équation des gaz parfaits par  ;
Toutes ces remarques nous conduisent à l’équation de Van der Waals caractéristique des gaz réels :
;
Toutes ces remarques nous conduisent à l’équation de Van der Waals caractéristique des gaz réels :
 (4)
(4)
3. Du gaz réel au gaz parfait
Rien de ce qui existe n’est parfait, le modèle du gaz parfait n’est qu’un modèle. Cependant un modèle doit refléter une certaine réalité, il est donc possible de considérer un gaz réel comme un gaz parfait, le but de ce paragraphe est d’expliciter les conditions pour lesquelles un gaz réel se comporte comme un gaz parfait. Nous avons vu que les molécules d’un gaz réel interagissent entre elles via l’interaction faible de Van de Waals, cette interaction est de courte portée, lorsque la distance entre les molécules augmente, elle tend ers zéro. Dans un gaz réel où les distances intermoléculaires sont très grandes, l’interaction de Van der Waals devient négligeable et par conséquent, les coefficients a et b disparaissent de l’équation (4) et on retrouve l’équation d’un gaz parfait. En conclusion un gaz réel peut être considéré comme parfait si l’espace offert aux molécules de ce gaz est grand. Ceci revient à dire que la pression au sein du gaz est faible. Le gaz parfait est un modèle qui permet de décrire les gaz réels sous de faibles pressions.4. Isotherme et échelle absolue de température
Nous avons défini précédemment l’échelle de température absolue en postulant l’existence d’un point fixe 273,15° plus bas que la température de fusion de la glace sous pression atmosphérique : le zéro absolu. Nous avons aussi défini la température cinétique d’un gaz parfait au paragraphe I de ce chapitre. Nous allons maintenant voir que la température cinétique peut nous permettre de définir une échelle de température qui coïncide avec l’échelle absolue. Pour cela imaginons le dispositif représenté figure 6.
Figure 6

Figure 7
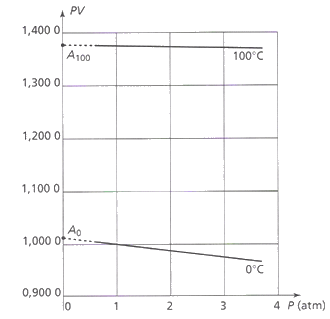
Figure 8


I. Le langage de la thermodynamique
1. Système thermodynamique
La thermodynamique permet l’étude de nombreux phénomènes si bien physiques que chimiques. Lors de cette étude la première chose à définir est le système thermodynamique. Le système thermodynamique constitue l’objet d’étude. Il est défini par séparation avec le milieu extérieur, cette séparation pouvant être matérielle ou non. On peut, par exemple considérer comme système thermodynamique un certain volume de fluide sans pour autant qu’il ne soit délimité par la paroi d’un récipient. Il existe divers termes qui qualifient un système thermodynamique. Système isolé : un système est dit isolé si il n’échange ni matière ni énergie avec le milieu extérieur. Système fermé : un système est dit fermé s’il n’échange pas de matière avec le milieu extérieur. Système ouvert : un système est dit ouvert s’il existe des échanges de matière entre le système et le milieu extérieur. Ces définitions montrent qu’un système thermodynamique est capable d’échanger des grandeurs avec le milieu extérieur, la convention qui est adoptée, ici, est la suivante : Toute grandeur reçue par le système est comptée positivement, toute grandeur cédée par le système est comptée négativement. Nous venons définir l’objet d’étude il nous faut maintenant être capable de décrire cet objet d’étude, ce système.2. Variables d’état
Considérons une mole d’eau, cette mole d’eau contient approximativement 1023 molécules. La description mécanique de ce système nécessiterait la donnée des coordonnées de position, des coordonnées de vitesse, de l’état de polarisation, de l’état de rotation et ce pour chaque molécule constituant le système. Le constat est donc effrayant, aucun ordinateur au monde ne serait capable de traiter un tel nombre de paramètres. Il semble donc que l’étude mécanique consistant à décrire chaque molécule individuellement soit à proscrire. Outre ce premier constat l’expérience nous montre que pour décrire l’état d’une mole d’eau, nous n’avons qu’à donner deux grandeurs : pression et température. Comment passe-t-on de 1023 paramètres à deux paramètres ? Telle est la question qu’on peut se poser. Pour y répondre il suffit d’imaginer le mouvement des molécules, c’est un mouvement désordonné, presque totalement aléatoire, de plus les molécules sont innombrables, et on peut procéder à une moyenne des grandeurs microscopique, de cette moyenne résulte les grandeurs macroscopiques auxquelles nous avons accès. En conclusion, l’état d’un système est décrit par un nombre restreint de paramètres macroscopiques. L’expérience permet de déterminer un nombre n de paramètres nécessaires et suffisant à la description du système : ce sont les n paramètres d’état. Une fois ces paramètres (ou variables d’état) fixés, l’état du système est parfaitement déterminé. Il existe divers types de paramètres d’état : - Les variables externes, ce sont les variables que l’expérimentateur peut ajuster. Il s’agit par exemple de la pression, de la quantité de matière ou de la température. - Les variables internes, ce sont des variables qui s’ajustent d’elles-mêmes à l’équilibre, on ne peut pas les fixer expérimentalement. - Les variables intensives, ce sont des variables qui ne dépendent pas de la taille du système (pression, température, concentration, tension). - Les variables extensives, ce sont des variables qui sont fonction de la taille du système (volume, charge) L’état du système peut donc être décrit par ces variables d’état, en revanche cette description n’est valable qu’à l’état d’équilibre thermodynamique.3. Etat d’équilibre
Prenons l’exemple d’un gaz enfermé dans un cylindre. Ce cylindre est fermé par un piston mobile de surface S. Si on pose sur ce piston une masse m. Sous l’action du poids, le piston va s’abaisser, osciller un peu autour d’une position et finalement s’y arrêter : le système aura alors atteint l’équilibre. Une fois qu’il est dans cet état on ne verra pas le piston remonter spontanément. Cette petite expérience nous permet d’énoncer en quelque sorte le postulat d’existence d’un état d’équilibre : Un système thermodynamique soumis à des contraintes extérieures uniformes et constantes évolue toujours vers un état d’équilibre qu’il ne peut plus ensuite quitter de manière spontanée. Cet état d’équilibre thermodynamique peut être décrit de la manière suivante : Un système est en état d’équilibre thermodynamique si les valeurs de ses variables d’état demeurent constantes au cours du temps et si lorsque le système n’est pas isolé il n’y aucune échange d’aucune sorte avec le milieu extérieur.4. Fonction d’état
Les variables d’états ne sont pas toutes indépendantes, elles sont liées entre elles par une fonction, c’est la fonction d’état. Une fonction d’état est une fonction des variables d’état, elle n’est donc dépendante que de l’état du système. Ces fonctions d’état possèdent des propriétés très importantes : - une fonction d’état n’est définie qu’à l’état d’équilibre thermodynamique - une fonction d’état est une différentielle totale exacte, ses dérivées secondes croisées sont égales. - La variation d’une fonction d’état est indépendante du chemin suivi. La toute dernière propriété revêt un caractère essentiel, c’est cette propriété qui nous permettra d’effectuer les calculs en thermodynamique.5. Transformations d’un système
Ne reste plus qu’à décrire l’évolution d’un système au cours du temps. Cette évolution peut en général s’interpréter en termes de transformations. On dit qu’un système thermodynamique subit une transformation lorsqu’il passe d’un état d’équilibre à un autre. Il existe diverses manières d’effectuer ce passage, il existe donc divers termes pour qualifier ces différentes transformations. - Transformation infinitésimale(ou élémentaire) : une transformation est dite infinitésimale lorsqu’elle entraîne une très faible variation des variables d’état. - Transformation quasi-statique : une transformation quasi-statique est une transformation qui se fait par une succession d’état d’équilibre du système. Lors d’une transformation quasi-statique, ce sont les différentes parties du système qui sont en équilibre entre elles, en revanche, il n’y a pas équilibre entre le système et le milieu extérieur (notamment équilibre thermique). - Transformation réversible : une transformation réversible est une transformation qui s’effectue par une succession continue d’état d’équilibre du système et du milieu extérieur - Transformation isochore : une transformation isochore est une transformation qui s’effectue à volume constant. - Transformation isobare : une transformation isobare est une transformation qui s’effectue à pression constante - Transformation isotherme : une transformation isotherme est une transformation qui s’effectue à température constante. - Transformation adiabatique : une transformation adiabatique est une transformation qui s’effectue sans échange de chaleur avec le milieu extérieur. Toutes les définitions que nous venons de donner sont relatives au système et aux transformations que celui-ci peut subir. Il temps, à présent, de présenter les grandeurs énergétiques qui sont susceptibles d’être échangées entre le système et le milieu extérieur.II. Travail
1. Définition
Considérons un point matériel se déplaçant d’un point A vers un point B. Ce point est soumis à une force . Lors de son déplacement, la force échange de l’énergie avec le point matériel. Si la force est motrice, le système reçoit de l’énergie (sa vitesse peut alors augmenter), sinon le système perd de l’énergie et la force est dite résistante.
Pour caractériser cet échange d’énergie entre système et milieu extérieur, on introduit la notion de travail d’une force. Le travail d’une force représente l’énergie échangée entre la force et le système auquel elle est appliquée. On définit le travail d’une force
. Lors de son déplacement, la force échange de l’énergie avec le point matériel. Si la force est motrice, le système reçoit de l’énergie (sa vitesse peut alors augmenter), sinon le système perd de l’énergie et la force est dite résistante.
Pour caractériser cet échange d’énergie entre système et milieu extérieur, on introduit la notion de travail d’une force. Le travail d’une force représente l’énergie échangée entre la force et le système auquel elle est appliquée. On définit le travail d’une force  sur un trajet AB par :
sur un trajet AB par :

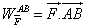
2. Travail des forces de pression
Commençons tout d’abord par rappeler l’expression de la force de pression. La pression est une force par unité de surface. Lorsqu’un fluide où règne une pression p est mis au contact d’une paroi il exerce sur cette paroi la force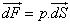 orientée vers la normale extérieure (c'est-à-dire du fluide vers la paroi).
Tentons maintenant d’exprimer le travail de ces forces de pression. Pour cela reprenons l’exemple d’un gaz enfermé dans un cylindre dont l’une des bases est constituée d’un piston mobile de surface S et où on étudie le système
orientée vers la normale extérieure (c'est-à-dire du fluide vers la paroi).
Tentons maintenant d’exprimer le travail de ces forces de pression. Pour cela reprenons l’exemple d’un gaz enfermé dans un cylindre dont l’une des bases est constituée d’un piston mobile de surface S et où on étudie le système 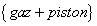 .
Exerçons une force
.
Exerçons une force  , sur le piston, il en résulte une pression extérieure sur le piston telle que
, sur le piston, il en résulte une pression extérieure sur le piston telle que  .Cette force provoque le déplacement du piston d’une distance dx. Le travail qui est alors fourni au système est :
.Cette force provoque le déplacement du piston d’une distance dx. Le travail qui est alors fourni au système est :
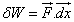
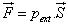

 car dx est négatif. Ce travail est fourni au système, il doit donc être positif, on écrira donc le travail des forces de pression :
car dx est négatif. Ce travail est fourni au système, il doit donc être positif, on écrira donc le travail des forces de pression :


3. Applications directes
Cas d’une transformation quasi-statique On considère une transformation réalisée de sorte qu’à tout instant, la pression à l’intérieur du gaz soit égale à la pression extérieure, on ne considère cependant pas que température extérieure et température du gaz sont égales : la transformation est alors quasi-statique. On considère cette fois-ci comme système le gaz. Le piston exerce sur le gaz la force dirigée du piston vers le gaz. Or pression extérieure et pression intérieure étant égale la force s’écrit aussi
dirigée du piston vers le gaz. Or pression extérieure et pression intérieure étant égale la force s’écrit aussi  où p est la pression du gaz.
En vertu du principe de l’action et de la réaction (3ème loi de Newton), le gaz exerce sur le piston la force
où p est la pression du gaz.
En vertu du principe de l’action et de la réaction (3ème loi de Newton), le gaz exerce sur le piston la force  dirigée du gaz vers le piston.
Lorsque le piston se déplace de dx, le travail reçu par le gaz est
dirigée du gaz vers le piston.
Lorsque le piston se déplace de dx, le travail reçu par le gaz est



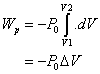
III. Transfert thermique. Chaleur
1. Aspect microscopique
Nous avons défini la température comme étant un nombre caractéristique de l’état thermique d’un corps. Cette définition est tout à fait exacte, donnons en maintenant une interprétation microscopique. En réalité, les composants microscopiques de la matière (solide, fluide ou mésomorphe) possèdent un mouvement désordonné, ce mouvement est appelé agitation thermique. Avec la température, ce mouvement devient de plus en plus important, si bien qu’on peut définir la température comme un nombre caractéristique de l’agitation thermique. Lorsque la température tend vers 0K, cette agitation tend à s’estomper et la matière à se figer. Voyons comment cette notion d’agitation thermique va nous permettre d’interpréter le transfert thermique.2. Transfert thermique
Mettons en contact un corps chaud et un corps froid. Les composants microscopiques du corps chaud sont plus agités que ceux du corps froid, de ce fait les composants microscopiques du corps froid situés à l’interface des deux corps vont se faire heurter par ceux du corps chaud et vont se mettre à vibrer de plus en plus, cette agitation se propage ainsi de proche en proche jusqu’à ce qu’elle devienne uniforme. La conséquence de cette propagation de l’agitation thermique est une diminution de la température du corps chaud et une augmentation de celle du corps froid. La propagation de l’agitation thermique s’accompagne d’une propagation de l’énergie thermique : il y a entre les deux corps transfert thermique. La quantité d’énergie thermique échangée est appelée chaleur. Là encore, la chaleur est une grandeur d’échange, elle n’existe que lors du transfert et devient nulle à l’équilibre thermodynamique.3. Capacités thermiques
Pour augmenter d’un degré Celsius la température d’un gramme d’eau à pression constante, il faut lui fournir 4,18 J. Pour réaliser la même augmentation de température avec un gramme de fer, il faut fournir une énergie de 0,455 J. Chaque corps n’accepte pas de la même manière l’énergie thermique. Donnons-en une interprétation microscopique. Plus les constituants microscopiques du corps sont distants et ont la possibilité de se déplacer facilement, plus cette substance pourra emmagasiner l’énergie thermique. En effet, les constituants étant éloignés et libres de se déplacer, ils ont peut de chance d’entrer en collision, or c’est cette collision qui provoque l’élévation de la température. D’une manière générale, il sera plus difficile d’augmenter la température d’un fluide que d’augmenter la température d’un solide. Pour quantifier la capacité d’un corps à emmagasiner de l’énergie thermique, on définit les capacités thermiques. Ces capacités thermiques relient la quantité de chaleur qu’on peut fournir au système et l’élévation de température qu’il en résulte. - A pression constante

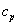 ou
ou  qui s’expriment en
qui s’expriment en 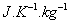 .
On rencontre aussi les capacités thermiques molaires
.
On rencontre aussi les capacités thermiques molaires 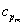 ou
ou  qui s’expriment en
qui s’expriment en 
I. Energie et thermodynamique
1. Diverses formes d’énergie
Pour fournir de l’énergie à un système, on dispose de deux processus que nous avons déjà présentés. Reprenons rapidement ces processus ici. En premier lieu, la mécanique newtonienne introduit le concept de travail d’une force. Ce travail correspond à la quantité d’énergie cédée par une force au système. Nous avons détaillé le cas des forces de pression, mais d’autres forces peuvent travailler : le poids, la force électrique, etc. L’énergie d’un système dépend aussi de l’agitation de ses composants microscopique, plus ceux-ci sont agité plus le système possède d’énergie thermique. Le système peut faire varier l’agitation thermique de ses constituants en échangeant avec le milieu extérieur de la chaleur, il réalise alors un transfert thermique. C’est en particulier ce type de transfert qui échappe à l’étude mécanique d’un système. La thermodynamique va corriger ce manque en introduisant un principe de conservation de l’énergie totale : le premier principe de la thermodynamique.2. Enoncé du premier principe
Considérons un système immobile et dont l’énergie potentielle ne varie pas (par exemple, l’altitude du système reste constante). Pour échanger de l’énergie avec le milieu extérieur, le système n’a que deux possibilité : travail et transfert thermique. Le premier principe s’écrit de la manière suivante: A tout système est associée une fonction d’état U appelée énergie interne. Au cours d’une variation quelconque, la variation d’énergie interne du système est égale à l’énergie reçue par le système.


3. Transformation isochore
Considérons un système S subissant une transformation isochore. Le volume du système est alors constant et noté V0. Le premier principe appliqué à une transformation infinitésimale de ce système s’écrit :
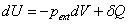
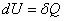

 s’identifie à la différentielle dU. Intéressons nous d’un peu plus près à cette identification.
A volume constant, on peut écrire :
s’identifie à la différentielle dU. Intéressons nous d’un peu plus près à cette identification.
A volume constant, on peut écrire :
 (1)
(1)
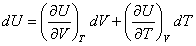
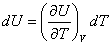 (2)
(2)
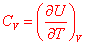
II. Transformation isobare. Enthalpie
1. Enthalpie
Considérons maintenant un système subissant une transformation isobare à la pression P0. Le premier principe appliqué à ce système aboutit à :
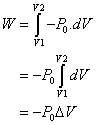 En introduisant cette expression dans l’énoncé du premier principe, on obtient :
En introduisant cette expression dans l’énoncé du premier principe, on obtient :
 (3)
(3)
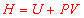

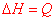
2. Capacité thermique à pression constante
On peut écrire l’enthalpie, H, comme une fonction de la température et de la pression, la différentielle de H s’écrit alors :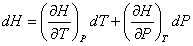
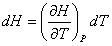 (4)
(4)

 (5)
(5)
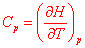
3. Différence entre Cp et Cv
Nous avons introduit deux capacités thermiques, l’une correspondant à des transformations isochores l’autre à des transformations isobares. On peut être en droit de s’interroger sur la nécessité de différencier ces deux coefficients. Nous allons tenter de justifier qualitativement la différence entre ces coefficients. Supposons que nous disposions d’une quantité de chaleur Q pour augmenter la température d’un système S. La question qu’on se pose est la suivante : vaut-il mieux travailler à pression constante ou à volume constant ? Faisons un rapide retour sur les thermomètres. Nombre d’entre eux utilisent la dilatation des corps avec la température (dilatation de solide, de liquides, de gaz). D’une manière générale, le volume d’un corps augmente avec la température et pour réaliser cette augmentation de volume, le système doit lutter contre les forces de pression. Du fait de ce phénomène, lorsqu’on se place à pression constante la quantité de chaleur Q sert non seulement à augmenter la température du système mais aussi à lutter contre les forces de pression. En revanche lorsqu’on maintient le système à volume constant, la quantité de chaleur Q ne sert qu’à faire augmenter la température du système. En conclusion, la capacité thermique à pression constante est toujours plus élevée que la capacité thermique à volume constant. Cependant, le phénomène de dilatation étant très faible pour les phases condensées (liquides, solides), on considère souvent que les capacités thermiques à pression constante et à volume constant sont égales pour les phases condensées. La relation qui lie Cp et Cv est la relation de Mayer :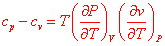
 est la capacité thermique massique à pression constante
-
est la capacité thermique massique à pression constante
-  est la capacité thermique massique à volume constant
-
est la capacité thermique massique à volume constant
- 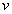 est le volume massique du système.
Nous reviendrons sur cette relation un peu plus loin dans le cours.
est le volume massique du système.
Nous reviendrons sur cette relation un peu plus loin dans le cours.
4. Enthalpie de changement d’état
Considérons un bêcher contenant un mélange eau glace placé sur une paillasse, on introduit dans ce bêcher un thermomètre. La transformation qui a lieu est une transformation isobare, le système reçoit de la chaleur du milieu extérieur, on devrait donc constater une élévation de la température selon la relation
reçoit de la chaleur du milieu extérieur, on devrait donc constater une élévation de la température selon la relation  . Or ce n’est absolument pas le cas l’indication donnée par le thermomètre est claire : il n’y a aucune variation de température. Qu’est donc devenue l’énergie fournie au système ?
Toute la chaleur fournie au système sert à réaliser le changement d’état. L’expression que nous avons citée plus haut n’est plus valable dans le cas d’un changement de phase. En effet, lors d’une fusion, la quantité de chaleur fournie au système s’écrit :
. Or ce n’est absolument pas le cas l’indication donnée par le thermomètre est claire : il n’y a aucune variation de température. Qu’est donc devenue l’énergie fournie au système ?
Toute la chaleur fournie au système sert à réaliser le changement d’état. L’expression que nous avons citée plus haut n’est plus valable dans le cas d’un changement de phase. En effet, lors d’une fusion, la quantité de chaleur fournie au système s’écrit :


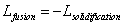 .
.
III. Le second principe
1. Nécessité d’un second principe
Le premier principe, nous l’avons vu, possède un caractère conservatif : une certaine grandeur appelée énergie se conserve au cours de la transformation d’un système thermodynamique. Ce principe permet de déterminer l’état final d’une transformation moyennant la connaissance de l’état initial et du chemin suivi lors de la transformation. Abordons maintenant une lacune fondamentale laissée par ce premier principe. Considérons une balle, assimilée à un point M de l’espace. Dans l’état initial, la balle se situe à la hauteur h1 au dessus du sol, ne possède pas de vitesse mais possède en revanche une énergie interne U1. Lorsqu’on lâche la balle, elle va chuter puis rebondir sur le sol, remonter, puis chuter à nouveau jusqu’à ce quelle s’immobilise sur le sol. Dans l’état final, la balle est à l’altitude h2, ne possède pas de vitesse mais possède une énergie interne U2. En notant : - l’énergie potentielle de la balle dans l’état initial
-
l’énergie potentielle de la balle dans l’état initial
-  l’énergie potentielle de la balle dans l’état final
Le premier principe de la thermodynamique appliqué à la balle s’écrit :
l’énergie potentielle de la balle dans l’état final
Le premier principe de la thermodynamique appliqué à la balle s’écrit :
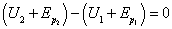
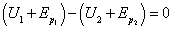
2. Notion d’irréversibilité
Nous sommes tous conscient, qu’il est impossible à la balle de remonter, il s’agit là d’une transformation irréversible. Pour combler la lacune laissée par le premier principe, c’est à cette notion d’irréversibilité qu’il faut s’intéresser. Nous allons donc tenter de trouver les diverses causes d’irréversibilité d’une transformation et nous verrons qu’il n’en existe qu’une qui se cache parfois sous divers aspects. Un exemple mécanique… Prenons pour système un palet. On lance ce palet sur une table horizontale avec une vitesse initiale v0. Au bout d’une certaine distance d, le palet s’immobilise… et ne reviendra jamais à sa position initiale quelque soit le temps qu’on attende : la transformation est irréversible. La cause de cette irréversibilité est la force de frottement, tout au long de la distance d, les frottements ont peu à peu consommé l’énergie cinétique du palet. Mais que sont ces frottements ? On décrit habituellement les frottements à l’aide d’un vecteur qu’on appelle vecteur force s’opposant au mouvement du solide. Mais regardons d’un peu plus près, chaque déplacement du palet s’accompagne d’un transfert d’énergie sous forme thermique du palet vers la table, la conséquence de ce transfert thermique est une augmentation de l’agitation des atomes constituant la table. En conclusion chaque déplacement du palet s’accompagne de la transformation du mouvement ordonné du palet en un mouvement désordonné des atomes. Un exemple chimique… On réalise la petite expérience suivante, une goutte de permanganate de potassium est lâchée dans un bêcher contenant 200mL d’eau. Au bout d’un certain temps, tout le bêcher acquiert une coloration mauve… et quelque soit le temps qu’on attende, il ne redeviendra pas spontanément incolore : c’est une transformation irréversible. La cause de cette irréversibilité est une certaine perte d’information. Avant que la goutte ne tombe dans le bêcher, on sait où sont les ions permanganates : ils sont dans le petit volume de la goutte. Lorsque le bêcher est mauve, les ions permanganate sont éparpillés dans les 200mL de liquide, leur localisation est beaucoup plus incertaine. En conclusion, l’irréversibilité de cette transformation est due à la perte de l’information « positions des ions permanganates ». On peut rassembler les résultats fournis par ces deux exemples de la manière suivante : L’irréversibilité d’une transformation trouve son origine dans la création de désordre ou dans la perte d’information. Le second principe de la thermodynamique que nous allons énoncer sous peu est basé sur cette interprétation de l’irréversibilité d’une transformation.3. Enoncé du second principe
L’énoncé du second principe peut prendre diverses formes équivalentes. Il postule l’existence d’une grandeur non conservative, l’entropie et précise son évolution. Tout système fermé est caractérisé par une fonction d’état extensive S appelée entropie, possédant pour une transformation infinitésimale la propriété suivante :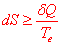
 est la chaleur reçue d’une source extérieure, Te la température de contact de cette source avec le système mesurée dans l’échelle thermodynamique. L’égalité à lieu lorsque la transformation est réversible.
L’inégalité exprimée par le second principe peut aussi s’écrire de la manière suivante :
est la chaleur reçue d’une source extérieure, Te la température de contact de cette source avec le système mesurée dans l’échelle thermodynamique. L’égalité à lieu lorsque la transformation est réversible.
L’inégalité exprimée par le second principe peut aussi s’écrire de la manière suivante :
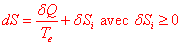
 est un terme d’échange, il représente la variation d’entropie sous l’effet d’un échange de chaleur avec le milieu extérieur.
Le terme
est un terme d’échange, il représente la variation d’entropie sous l’effet d’un échange de chaleur avec le milieu extérieur.
Le terme 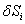 est l’entropie créée lorsque la transformation n’est pas réversible, il met en relief le caractère non conservatif de l’entropie : l’entropie peut être créée à l’intérieur du système lors d’une transformation. Le terme
est l’entropie créée lorsque la transformation n’est pas réversible, il met en relief le caractère non conservatif de l’entropie : l’entropie peut être créée à l’intérieur du système lors d’une transformation. Le terme  , permet de quantifier l’irréversibilité d’une transformation, plus il y a d’entropie créée, plus la transformation est irréversible.
La fonction entropie S est une fonction d’état, de ce fait elle n’est définie que pour des états d’équilibre du système. On peut exprimer l’entropie à l’aide de divers jeux de variables, mais il existe un système de variables simples (les variables naturelles de S) permettant à la fonction entropie de contenir toute l’information sur le système, ces variables sont :
- U l’énergie interne
- n la quantité de matière
- V le volume
On peut ainsi exprimer simplement l’extensivité de la fonction entropie :
, permet de quantifier l’irréversibilité d’une transformation, plus il y a d’entropie créée, plus la transformation est irréversible.
La fonction entropie S est une fonction d’état, de ce fait elle n’est définie que pour des états d’équilibre du système. On peut exprimer l’entropie à l’aide de divers jeux de variables, mais il existe un système de variables simples (les variables naturelles de S) permettant à la fonction entropie de contenir toute l’information sur le système, ces variables sont :
- U l’énergie interne
- n la quantité de matière
- V le volume
On peut ainsi exprimer simplement l’extensivité de la fonction entropie :
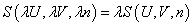
 est S=SA+SB.
est S=SA+SB.
4. Cas d’un système isolé
L’énoncé du second principe se simplifie notablement dans le cas d’un système isolé. En effet, pour un système isolé, la quantité est toujours nulle, ce qui conduit pour une transformation infinitésimale à :
est toujours nulle, ce qui conduit pour une transformation infinitésimale à :

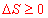
5. Calcul d’une variation d’entropie
Tout comme le premier principe permet le calcul d’une variation d’énergie interne, le second principe permet le calcul d’une variation d’entropie. Soient deux états d’équilibre du système A et B, la variation d’entropie d’un système passant d’un état A à l’état B peut se calculer à une seule condition : il faut être capable d’imaginer une transformation réversible allant de A jusque B. Si cette transformation est possible, on peut écrire:
 , de plus
, de plus  , il en résulte que la variation d’entropie du système est nulle. Toute transformation adiabatique réversible est isentropique.
- la variation d’entropie d’un thermostat. Un thermostat est un système modèle toujours en équilibre interne à la température T0. Pour un tel système tout transfert thermique est réversible, si on note Q0 la quantité de chaleur échangée avec l’extérieur , sa variation d’entropie est
, il en résulte que la variation d’entropie du système est nulle. Toute transformation adiabatique réversible est isentropique.
- la variation d’entropie d’un thermostat. Un thermostat est un système modèle toujours en équilibre interne à la température T0. Pour un tel système tout transfert thermique est réversible, si on note Q0 la quantité de chaleur échangée avec l’extérieur , sa variation d’entropie est 
6. Identité thermodynamique
Prenons comme système un fluide homogène (un gaz parfait par exemple). Pour une transformation réversible, le second principe s’écrit :

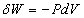
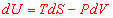
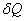 et
et 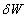 respectivement.
Deux conséquences découlent de cette identité :
respectivement.
Deux conséquences découlent de cette identité :
- Les variables naturelles de U sont S et V, on peut ainsi écrire par identification
 et
et 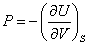
- L’identité peut être utilisée pour expliciter dS, , on en déduit alors que les variables naturelles de S sont U et V, et on peut écrire
 et
et 
IV. Calculs d’entropie
1. Le troisième principe de la thermodynamique
Le second principe que nous avons énoncé ne nous donne accès qu’à des variations d’entropie, de ce fait, la fonction d’état entropie n’est définie qu’à une constante additive près. Si on donne une valeur à cette constante, on pourra avoir accès non plus à une variation d’entropie mais à l’entropie absolue d’un système. Cette constante est fixée par le troisième principe de la thermodynamique. Lorsque la température d’un corps tend vers le zéro absolu, son entropie tend vers une valeur limite qui est indépendante de la pression et des autres paramètres définissant l’état du système. Pour les solides cristallisés on attribue par convention à cette limite la valeur 0. Ce choix n’est pas tout à fait arbitraire, nous avons vu au début de ce chapitre que l’entropie reflétait la notion de perte d’information ou de désordre. Or, au zéro absolu, l’agitation moléculaire est quasi-inexistante, la localisation des constituants microscopique de la matière est donc de la meilleure précision possible : la perte d’information est minimale, l’entropie tend donc vers 0.2. Calcul d’entropie
L’union du deuxième et du troisième principe nous donne accès à l’entropie d’une mole de cristal à la température T. En effet, la variation d’entropie entre le zéro absolu et la température T est donnée par :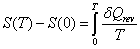



 les termes correspondant au changement d’état. Si on note Li la chaleur latente de changement d’état, et Ti la température de ce même changement d’état, l’expression précédente devient :
les termes correspondant au changement d’état. Si on note Li la chaleur latente de changement d’état, et Ti la température de ce même changement d’état, l’expression précédente devient :

V. Fonctions thermodynamique et sens d’évolution
1. Energie libre
Jusque là, nous avons introduit trois fonctions d’état permettant de décrire un système thermodynamique : - l’énergie interne U dont les variables naturelles sont S,V (et n) - l’enthalpie H dont les variables naturelles sont S, P (et n) - l’entropie dont les variables naturelles sont U,V (et n) On remarque que l’entropie intervient dans chacune de ces fonctions, or expérimentalement, on n’a pas accès à l’entropie. En conséquence, lorsque les variables expérimentales sont la température et le volume, on introduit l’énergie libre F définie par F=U-TS. La différentielle de F s’écrit alors :
2. Enthalpie libre
Lorsque les variables expérimentales sont la température et la pression, ce qui est majoritairement le cas dans l’étude des réactions chimiques, on introduit l’enthalpie libre définie par G=H-TS. La différentielle de G s’écrit alors :
3. Evolution et équilibre
En observant l’expression de la différentielle dG (ou dF), on remarque que la variation de l’enthalpie libre (resp. énergie libre) se fait en sens opposé à la variation d’entropie. En conséquence, un système évoluera toujours de manière à ce que son enthalpie libre diminue. Cette propriété important de l’enthalpie libre lui confère les propriétés d’un potentiel. En effet tout comme l’énergie potentielle de pesanteur tend à diminuer lorsqu’on abandonne une balle à une hauteur h1, l’enthalpie libre tend à diminuer lorsqu’on abandonne un système en contact avec l’atmosphère à la pression P0 et la température T0. L’équilibre sera atteint lorsque l’enthalpie libre sera minimale.I. Généralités
1. Définition thermodynamique
En thermodynamique tout système réalisant la conversion de l’énergie thermique en énergie mécanique est appelé machine thermique. Le terme machine thermique rassemble le réfrigérateur, le moteur ou encore la pompe à chaleur. Les plus simples de ces machines sont les machines cycliques dithermes, ce sont des systèmes fermés évoluant de manière cyclique entre deux sources de température : une source chaude à la température Tc et une source froide à la température Tf. Dans le cas des moteurs on donne de l’énergie thermique (Qc) au système via la combustion du carburant et il produit à partir de cette énergie du travail (W) tout en cédant une partie de l’énergie thermique à la source froide (Qf).
 la quantité de chaleur échangée avec la source chaude
-
la quantité de chaleur échangée avec la source chaude
-  la température de la source chaude
-
la température de la source chaude
-  la quantité de chaleur échangée avec la source froide
-
la quantité de chaleur échangée avec la source froide
-  la température de la source froide
Et nous considérerons que tout ce qui est reçu par le système est compté positivement, tout ce qui est cédé par le système est compté négativement.
la température de la source froide
Et nous considérerons que tout ce qui est reçu par le système est compté positivement, tout ce qui est cédé par le système est compté négativement.
2. Efficacité d’un moteur thermique
Comme tout système voué à la grande consommation ou à l’industrie, une machine thermique est caractérisée par son rendement, qu’on appellera aussi efficacité thermodynamique de a machine. Cette efficacité est définie comme étant le rapport de la grandeur valorisable (i.e. la grandeur qu’on cherche à récupérer) sur la grandeur couteuse (i.e. la grandeur qu’on doit fournir pour que la machine fonctionne).

 est bel et bien positif.
De manière générale, un rendement est toujours inférieur à 1, mais la thermodynamique a ses particularités et le rendement d’une machine thermique peut parfois excéder 1 (cf. Pompes à chaleur) la question qui se pose alors est la suivante : « comment peut-on savoir si un moteur a un bon rendement ? à quelle valeur comparer son efficacité thermodynamique ? ». La réponse à cette interrogation vient de l’application des deux principes de la thermodynamique aux machines thermiques.
Commençons par le premier principe :
est bel et bien positif.
De manière générale, un rendement est toujours inférieur à 1, mais la thermodynamique a ses particularités et le rendement d’une machine thermique peut parfois excéder 1 (cf. Pompes à chaleur) la question qui se pose alors est la suivante : « comment peut-on savoir si un moteur a un bon rendement ? à quelle valeur comparer son efficacité thermodynamique ? ». La réponse à cette interrogation vient de l’application des deux principes de la thermodynamique aux machines thermiques.
Commençons par le premier principe :

 On obtient donc :
On obtient donc :
 (1)
(1)



 (2)
(2)





II. La machine à vapeur
1. Principe de fonctionnement
Dans un moteur quelqu’il soit, le but premier est de déplacer un piston c'est-à-dire de produire du travail en fournissant de l’énergie thermique au système. Pour réaliser cette transformation, l’idée de base est de provoquer une variation brusque de pression suffisante pour déplacer le piston, chacun des moteurs que nous allons décrire est exploite un moyen de réaliser cette variation de pression. Les premiers moteurs qui furent développés furent les machines à vapeur. Datant du XVIIème siècle ces machines s’appuient sur la variation énorme de volume occupé par la vapeur d’eau et par l’eau liquide, l’idée est la suivante : si on enferme de la vapeur d’eau dans un cylindre fermé par un piston mobile et qu’on refroidit ce cylindre, la vapeur d’eau se liquéfie faisant chuter la pression dans le cylindre et la variation de pression alors imposée provoque le déplacement du piston ! Les machines à vapeur s’appuie donc sur la vaporisation et la liquéfaction successives de l’eau à travers les éléments suivants: - D’un compresseur - D’une chaudière - D’un cylindre moteur - D’un condenseur
2. Etude thermodynamique
Le cycle de la machine à vapeur porte le nom de cycle de Rankine, il est facilement représentable dans le diagramme T-s.
 où on a noté en minuscule les grandeurs massiques.
- La quantité de chaleur Qc a été fournie au fluide dans la chaudière, on a alors :
où on a noté en minuscule les grandeurs massiques.
- La quantité de chaleur Qc a été fournie au fluide dans la chaudière, on a alors : Le rendement de la machine à vapeur ainsi constituée est donc :
Le rendement de la machine à vapeur ainsi constituée est donc :


III. Le moteur de Stirling
1. Principe de fonctionnement
Au temps des machines à vapeurs nombreuses étaient les explosions… pour améliorer la sécurité des personnes un autre moteur fit son apparition le moteur Stirling. Dans un moteur de stirling une même quantité de gaz reçoit un transfert thermique Qc d’une source chaude à la température Tc=1500K (maintenue constante grâce à la combustion continue d’un combustible) et cède l’énergie thermique Qf à une source froide à la température Tf=320K (circuit de refroidissement). Dans la configuration beta du moteur de stirling, le moteur est constitué d’un cylindre dans lequel deux pistons peuvent se déplacer : - Un piston de déplacement qui détermine la répartition du gaz entre la source chaude et la source froide - Un piston de travail qui impose les variations de volume total du gaz et par le bieais duquel on récupère l’énergie mécanique Les chambres chaudes (C) et Froides (F) sont reliées par un régénérateur (R) servant à récupérer l’énergie thermique du gaz qui le traverse, à la stocker et à la lui restituer ultérieurement. Ainsi lorsque le gaz passe de C vers F le gaz se refroidit de la température Tc à la température Tf en cèdant au régénérateur l’énergie thermique Qr. Au contraire lorsqu’il passe de F vers C, il se réchauffe de Tf jusque Tc en recevant le transfert thermique Qr. C’est la capacité du régénérateur à échanger à chaque fois la même énergie thermique avec le gaz qui déterminera l’efficacité du moteur.2. Etude thermodynamique
Prenons comme instant initial (A) l’instant où le volume du gaz est minimal Vmin= 0,10L et où il est en contact avec la source chaude à la température Tc. Sous l’action de la source chaude, le gaz va se détendre jusqu’à atteindre son volume maximal et comme cette détente a lieu au contact de la source chaude, il s’agit d’une isotherme à al température Tc on notera alors B le point représentatif de l’état du système. Lors de cette étape les deux pistons ont été solidairement repoussés vers le bas du cylindre. Le piston de travail restant fixe, le volume total étant par conséquent constant, le piston de déplacement force le gaz à passer dans le régénérateur R où il subit un refroidissement isochore. Le système aboutit donc à l’état C sous une pression de 1bar et la température Tf. Le piston de déplacement restant fixe cette fois, c’est au tour du piston de travail de se déplacer ; il remonte en comprimant le gaz de manière isotherme au contact de la source froide l’amenant ainsi à son volume minimal . Enfin le piston de travail restant fixe, le piston de déplacement redescend provoquant le passage du gaz à travers le régénérateur et ramenant le système à son état initial. Le gaz subissant les transformations cycliques pouvant être assimilé à un gaz parfait diatomique, on peut calculer la quantité de matière de gaz dans le cylindre en utilisant l’état C :







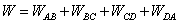



IV. Les moteurs essence atmosphériques
1. Principe de fonctionnement
Un moteur à explosion comporte un certain nombre de cylindres appelé chambre (de 1 à 12). A l’intérieur de ces cylindres peuvent se déplacer les pistons. Chacun des pistons est relié, à la base, au vilebrequin, il s’agit d’une sorte d’axe qui coordonne le mouvement des pistons et qui relie le moteur à la transmission. A l’extrémité supérieure du cylindre se trouvent les soupapes, il s’agit de « clapets » qui s’ouvrent et se ferme en fonction des besoins du moteur. Il existe deux types de soupapes : - la soupape d’admission qui laisse entrer le carburant - la soupape d’échappement qui permet aux gaz brûlés de s’échapper Toujours à l’extrémité supérieure du cylindre se trouve une bougie, il s’agit d’une source d’étincelle qui permet de déclencher la combustion du mélange air-carburant au moment opportun. Le moteur à explosion (essence) comporte quatre temps : - Premier temps, l’admission. Partant du point mort haut, le piston, entraîné par le vilebrequin, descend progressivement en aspirant le mélange air-essence par la soupape d’admission. Pendant ce temps, la soupape d’échappement reste fermée. Lorsque le piston arrive en bas de course (point mort bas), la soupape d’admission se referme, et les deux soupapes resteront ainsi fermées pendant les deux temps qui suivent. - Deuxième temps, compression. Le piston remonte en comprimant le mélange. - Troisième temps, explosion-détente. Une étincelle à la bougie provoque l’explosion du mélange, le piston se retrouve ainsi repoussé jusqu’au point mort bas communiquant un mouvement de rotation au vilebrequin. Ce temps constitue la phase proprement motrice. - Quatrième temps, échappement. La soupape d’échappement s’ouvre, et le piston en remontant chasse les gaz brûlés dans l’atmosphère extérieure. Le cycle peut alors recommencer.2. Etude thermodynamique
Nous allons tenter de modéliser chacune des étapes du cycle par une transformation réversible de sorte à pouvoir représenter ce cycle dans le diagramme de Clapeyron. On utilisera donc le modèle suivant : - Admission (A0A). Le mélange qui est aspiré provient de l’extérieur, cette phase se fait à pression constante (celle imposée par la descente du piston), l’admission est une étape isobare à P1=1bar. - Compression (AB). La compression a lieu très rapidement, suffisamment rapidement pour qu’on puisse négliger tout échange thermique, la compression est une étape adiabatique. A la fin de la compression la pression dans le cylindre est de l’ordre de 18bar et le volume du cylindre est le volume minimal Vmin=0,25L. - Explosion (BC+CD). Si on suppose que le piston n’a pas le temps de se déplacer durant l’explosion, le gaz subit alors une élévation de température à volume constant, la pression dans le cylindre atteint alors 45bars. Ensuite le piston se déplace rapidement jusqu’au point mort bas où le volume occupé est le volume maximal Vmax=2L ce que nous modéliserons par une détente adiabatique. Le troisième temps est donc constitué d’une isochore et d’une adiabatique. - Echappement (DA). On supposera enfin que le gaz se refroidit instantanément jusque la température initiale avant d’être refoulé à l’extérieur, il s’agit donc d’une transformation isochore (DA) qui ramène le système à une température Ti=100°C. Ces transformations aboutissent au cycle suivant :




 , on en déduit alors :
, on en déduit alors :
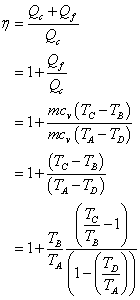

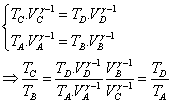




3. Avantages et inconvénients
Le rendement théorique que nous avons établi représente de manière tout à fait exacte l’évolution du rendement avec le taux de compression. Augmenter ce taux de compression semble donc un bon moyen d’augmenter les performances d’un moteur, cette voie comporte cependant deux limites majeures : - Un taux de compression élevé implique une résistance mécanique des pistons et des soupapes qui ne peut pas être accrue indéfiniment, la limite est généralement atteinte lorsque le taux de compression est voisin de 9 - A une pression trop élevée , correspond une température élevée et lorsque la température est trop élevée, la combustion a lieu trop tôt dans le cylindre et tout le carburant n’est pas brulé, on assiste donc à une combustion incomplète. On voit aussi apparaitre le phénomène de cliquetis correspondant un à une combustion dans le cylindre débutant non pas au niveau de la bougie mais en un autre point du cylindre. Les moteurs essences sont à cause de la légèreté des composants mécaniques et du caractère instantané de l’explosion des moteurs très réactifs à bas régime. La contrepartie c’est une consommation parfois excessive notamment due au phénomène de combustion incomplète.V. Le moteur Diesel
1. Principe de fonctionnement
Inventé par l’ingénieur allemand Rudolf Diesel en 1893, ce moteur est comme le précédent un moteur à quatre temps. L’architecture diffère peu du moteur à explosion. On constate la disparition de la bougie qui est remplacée par un autre type de bougie (bougie de chauffage) dont nous ne préoccuperons pas ici. On notera aussi la présence d’injecteurs servant à introduire le carburant dans le cylindre. Les quatre temps sont les suivants : - Premier temps, admission. Cette phase est semblable à celle du moteur essence mais cette fois-ci seul l’air est aspiré. - Deuxième temps, compression. Temps en tout point identique à la compression dans un moteur essence. - Troisième temps : combustion-détente. Le combustible est injecté sous pression en haut du cylindre. A la température élevée de l’air comprimé, l’inflammation se produit spontanément. La combustion se réalise alors progressivement en produisant des gaz, lorsque la combustion s’arrête, les gaz se détendent alors ce qui constitue la phase motrice. - Quatrième temps. C’est une phase identique à celle du moteur à explosion.2. Etude thermodynamique
Une fois encore, nous assimilerons encore les gaz à des gaz parfaits et chacune des transformations à une transformation réversible. On modélise les différentes étapes par le modèle suivant : - Admission : transformation isochore A





 et
et  .
Dans notre exemple, on peut calculer :
.
Dans notre exemple, on peut calculer :- Le travail sur le cycle W=-2,7kJ
- La quantité de chaleur fournie par la source chaude Qc=4kJ
Il en résulte un rendement de 0,68 ce qui est bien meilleur que le rendement d’un moteur essence. De même on peut calculer la puissance de ce moteur à 4000tr/min, et on aboutit à 125ch !!
3. Avantages et inconvénients
Le moteur diesel a meilleur rendement que le moteur essence, ce qui marque le premier avantage de ce moteur. La grosse différence se fait à bas régime, en effet les pièces d’un moteur diesel se doivent d’être bien plus robuste en raison des pressions élevées et de ce fait l’inertie du moteur est plus grande : le moteur diesel est un moteur lourd ! D’autre part l’injection et la combustion sous pression constante est la cause de l’augmentation du rendement mais c’est aussi la cause d’une moins bonne réactivité que le moteur essence, car cette combustion isobare demande plus de temps que l’explosion des moteurs essences.
L'électricité, est la science qui nous permet de comprendre le fonctionnement des appareils électriques que nous cotoyons quotidiennement. Vous y apprendrez que des particules invisiblent circulent constamment dans les conducteurs, qu'il y a diverses façon de fabriquer un circuit électrique mais que pour faire un circuit il faut toujours des composants! C'est en associant correctement les divers composants que vous découvrirez que vous pourrez fabriquer un circuit électrique fiable et opérationnel, le tout étant d'éviter d'électrocuter qui que ce soit!
L'électromagnétisme, est la science qui étudie l'action des particules chargée, des courants et des ondes que ceux-ci peuvent créer. Avant de parler d'électromagnétisme à proprement parler, il vous faudra étudier les charges fixes : c'est le role de l'électrostatique. Ensuite, il vous faudra étudier les courants permanents: c'est la magnestostatique. C'est seulement avec ces bases que vous pourrez vous attaquer à l'électromagnétisme, c'est à dire à la propagation des ondes électromagnétiques telles que la lumière ou les ondes radio. Vous comprendrez par exemple comment fonctionnent les radars, mais ne comptez pas les éviter!
La mécanique, est la science qui nous permet de comprendre le mouvement des objets qui nous entourent. De la simple pomme qui tombe de l'arbre au mouveemnt des planètes et des étoiles qui constellent nos nuits! Vous apprendrez ici à décrire les trajectoires des corps en mouvement puis en vous appuyant sur l'observation du passé vous découvrirez peu à peu comment on peut prédire l'avenir! Enfin, en ce qui concerne la position de ceux-ci, n'espérez pas gagner au loto grace à la mécanique...
L'optique, est la science qui vous aidera à comprendre ce que vous voyez! Dans un monde où l'apparence est si importante vous y découvrirez comment le sinstruments d'optique sont conçus pour améliorer notre vision des choses, comment l'oeil humain fonctionne et quels sont ses défauts. Enfin vous saurez expliquer l'arc en ciel et ces couleurs étranges qui peuvent apparaitre lorsque la lumière traverse un rideau ou se réfléchi sur une flaque d'huile..
La radioactivité, est la science qui s'intéresse à la stabilité de la matière. Vous y ferez un voyage au coeur de la matière jusqu'au centre de l'atome oùvous rencontrerez le noyau atomique et les quarks qu'il contient. Vous apprendrez que la matière n'est pas toujours stable et que pour remédier à cette instabilité la nature a trouvé un moyen: les réactions radioactives! Enfin vous verrez que l'Homme exploite aussi cette instabilité de la matière en provoquant des réactions nucléaires ! la fission et la fusion!
La spectrométrie, est une méthode d'analyse non destructive de la matière. Elle permet de sonder le coeur des molécules, d'identifier les liaisons entre composés voire les liaisons au sein d'un même composé. Il existe diverses méthodes spectroscopiques qui diffèrent par l'énergie de l'onde qu'on envoie sur la matière et donc par l'objectif de l'analyse spectroscopique.
La thermodynamique, science universelle qui rassemble la mécanique et les échanges thermiques, elle permet de définir l'état d'équilibre d'un système, d'en prévoir l'évolution qu'il s'agisse d'un système physique ou chimique!

