I. Généralités

1. Définition

Un capteur optique transforme l’énergie lumineuse en énergie électrique, tous les capteurs que nous allons voir sont par conséquent des capteurs de flux lumineux. L’action d’un capteur optique est représentée par le schéma de la figure 1.

Figure 1

Ce chapitre aura deux objectifs principaux : - d’une part il nous faut comprendre comment se fait la conversion énergie lumineuse/énergie électrique - d’autre part il nous faut caractériser la réponse, du capteur, répond il toujours de la même manière ? de quoi dépend cette réponse. En réalité ces deux problématiques sont liées, comme nous allons le voir, c’est le principe de conversion qui détermine en majeure partie la réponse du capteur, mais il existe un autre facteur déterminant de la réponse : le conditionnement du capteur.

2. Les deux types de capteurs

Imaginons que nous soyons des inventeurs chevronnés du début du XXème siècle. Et que nous ayons pour mission de construire des capteurs optiques. Or si vous voulez capter quelque chose, la première question que vous devez vous poser porte sur la nature de ce que vous voulez capter ; première question : qu’est ce que la lumière ? A cette question nous répondons : la lumière est une onde électromagnétique. Bien, nous savons maintenant que la lumière est une onde, comment déceler cette onde ? Pour répondre à cette question, nous devons trouver comment agit une onde électromagnétique sur la matière… réalisons donc une petite expérience. On place une petite plaque noire au soleil durant quelques instants. Lorsqu’on revient : la température de la plaque a considérablement augmentée. On en déduit qu’une onde électromagnétique a la faculté de provoquer une variation de température d’un corps qui la reçoit. Nous venons de trouver une première méthode de détection de la lumière qui est à l’origine d’un premier type de capteur : les capteurs thermiques. Propulsons nous maintenant quelques dizaines d‘années plus tard, après l’intervention de Einstein, Schrödinger, Pauli et Dirac. La mécanique quantique est alors bien établie, et la physique se base maintenant sur la quantification. La lumière n’est plus vue comme une onde mais comme un ensemble de particules sans masse se déplaçant à la vitesse c et d’énergie : les photons. Ce que nous devons capter ce n’est donc plus une onde mais une particule. La démarche est la même, il nous faut savoir comment agit un photon lorsqu’il arrive sur la matière, c’est de cette manière que nous pourrons mettre en œuvre un capteur. Les expériences pour mettre en évidence cette action sont un peu plus délicates à réaliser, mais d’une manière générale, on peut dire qu’un photon a la faculté de faire passer un électron de la matière dans un état excité, c’est l’effet photoélectrique. Et nous voilà avec une idée de génie : si on arrive à récupérer cet électron, et à le faire circuler dans un circuit, nous obtiendrons un courant. C’est le principe des détecteurs photoniques.

3. Caractéristiques d’un capteur

Quel qu’il soit : photonique ou thermique, un capteur optique est caractérisé par les mêmes grandeurs. - La sensibilité C’est une caractéristique fondamentale des capteurs que nous appliquons aux capteurs optiques. Soit un capteur recevant un flux lumineux, F, la réponse de ce capteur est R (courant ou tension), on définit alors la sensibilité par :

La sensibilité s’exprime en volt/watt ou en ampère/watt. - Le temps de réponse Le temps de réponse est aussi une caractéristique fondamentale des capteurs. Il s’agit du temps caractéristique d‘évolution du signal électrique fourni par le capteur lorsque le flux varie brusquement. Nous verrons comment on le détermine en Travaux Pratiques et nous reviendrons sur son importance dans les spectromètres dans les chapitres suivants. - La linéarité Un capteur est dit linéaire si le signal de sortie est proportionnel au flux reçu. En général il n’y a linéarité que sur une certaine gamme . Un capteur linéaire est commode d’utilisation, mais la linéarité n’est pas nécessaire pour utiliser un capteur, un capteur est exploitable une fois qu’on connaît sa réponse qu’elle soit linéaire ou pas. - La réponse spectrale Tout comme un système électrique possède une bande passante, la réponse d’un capteur optique est fonction de la longueur d’onde de la lumière incidente. Un capteur ne répond pas de la même manière dans l’infrarouge et dans l’ultraviolet. On notera donc plus généralement la réponse d’un capteur . Remarque : Il découle de cette propriété que la sensibilité est aussi fonction de la longueur d’onde. - Le rendement quantique C’est une caractéristique propre aux détecteurs photoniques. Nous avons vu que dans ces capteurs, un photon incident provoquait l’excitation d’un électron. En réalité un photon incident ne provoque pas l’excitation d’un électron mais de 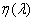électrons. 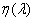est le rendement quantique, il s’agit du nombre d’électron excités pour un photon incident.

II. Les capteurs photoniques

1. Deux types de capteurs photoniques

Nous commencerons par les capteurs photoniques car ce sont de loin les plus courants de nos jours. Lorsqu’un photon arrive sur ces capteurs, il provoque l’excitation d’électrons, on différenciera deux types de capteurs photoniques suivant le devenir de cet électron : - Soit l’électron reste dans le matériau, et le capteur est dit à effet photoélectrique interne. C’est le cas de tous les capteurs à semi-conducteur. - Soit l’électron est éjecté hors du matériau et le capteur est dit à effet photoélectrique externe. C’est le cas du photomultiplicateur. Dans cette partie, nous donnerons une large place aux détecteurs à semi-conducteurs, car, une fois encore, ce sont les plus courants. Nous détaillerons ensuite le principe de fonctionnement du photomultiplicateur car il est utilisé dans certains spectromètres et possède une sensibilité remarquable.

2. Principe des capteurs à semi-conducteurs

Les semi-conducteurs sont des matériaux tout à fait remarquables, ils sont parfois isolants et parfois conducteurs. Revenons quelques instants sur la structure de ces matériaux. - Semi-conducteur homogène Nous savons, depuis l’élaboration de la théorie quantique que les niveaux énergétiques sont quantifiés. Dans un matériau semi-conducteur, il existe deux bandes d’énergie : - une bande de valence pleine d’électrons - une bande de conduction totalement vide à T=0K et à l’équilibre. Ces bandes d’énergies sont séparées par un intervalle où aucun niveau d’énergie n’existe : c’est le GAP du semi-conducteur. Lorsque la bande de valence est pleine, le matériau est isolant car les électrons ne peuvent pas se déplacer librement. Pour qu’un électron assure la conduction du courant, il doit passer de la bande de valence à la bande de conduction. En effet lorsqu’un électron se retrouve dans la bande de conduction, il peut prendre tous les niveaux d’énergie de cette bande et peut donc se déplacer dans le matériau : c’est cette liberté des électrons de la bande de conduction qui est responsable de la conduction dans les semi-conducteurs. Mais quel est le prix de cette liberté ? Pour passer de la bande de valence à la bande de conduction, l’électron doit traverser le GAP, il doit donc posséder l’énergie nécessaire pour réaliser ce saut. L’énergie peut être fournie de diverses manières : - énergie thermique - énergie lumineuse, c’est un photon qui permet le passage (c’est ce qui nous intéresse ici) On peut donc imaginer le capteur suivant : Un matériau semi-conducteur est exposé à un rayonnement, lorsqu’un photon entre en contact avec le matériau, un électron passe de la bande de valence à la bande de conduction ce qui provoque l’apparition d’un courant dans le matériau. Remarque : lors du passage d’un électron de la bande de valence à la bande de conduction celui-ci laisse derrière lui (dans la bande de valence) un trou qui va aussi participer à la conduction. Nous verrons que ce capteur est effectivement opérationnel mais il possède un temps de réponse plutôt médiocre, de ce fait les capteurs les plus performants ne sont pas fait d’un seul semi-conducteur homogène mais de deux semi-conducteurs. -Dopage type N et dopage type P Il est très courant d’ajouter à un semi-conducteur tel que le Silicium un atome d’arsenic (As), on dit alors qu’il est dopé N. Voyons qualitativement l’effet de ce dopage. Le silicium possède quatre électrons de valence alors que l’arsenic en possède cinq. Il existe donc dans le matériau des électrons très peu liés et par conséquent fort enclin à passer dans la bande de conduction. A température ambiante, tous ces électrons sont passés dans la bande de conduction et le matériau possède un excès de porteurs de charge négatifs d’où le nom « dopé N ». Par ailleurs, il est tout aussi courant d’ajouter au silicium des atomes de bore. Le bore étant trivalent, le matériau se retrouve avec des trous (charges positives) dans la bande de valence, on dit qu’il est dopé P. -Jonction PN Voyons maintenant ce qu’on obtient si on rassemble un semi-conducteur dopé N et un semi-conducteur dopé P. Les charges négatives du dopé N vont être attirés par le dopé P, inversement les charges positives du dopé P vont être attirés par le dopé N. Il y a donc un mouvement de charge qui s’arrête lorsque les charges se sont toutes déplacées, il existe alors au niveau de la jonction un champ électrique dirigé du semi-conducteur dopé N vers le semi-conducteur dopé P (cf. Figure 1).

Figure 2

Ce dispositif est à l’origine de la diode, mais nous ne nous attarderons pas sur cet aspect ici, puisque ce qui nous intéresse ce sont les capteurs optiques, voyons comment cette jonction peut être utilisée pour fabriquer le capteur optique le plus courant : la photodiode.

3. La photodiode

Une photodiode est une jonction PN à base de silicium. Lorsqu’un photon arrive sur la jonction PN, il est absorbé et provoque la création d’une paire électron-trou. Le champ électrique qui règne au niveau de la jonction sépare les porteurs de charge : l’électron se déplace vers la zone P et le trou vers la zone N. -Photodiode en circuit ouvert En circuit ouvert, les électrons et les trous créés par les photons s’accumulent de part et d’autre de la jonction, il apparaît donc une différence de potentiel au borne de la photodiode : c’est l’effet photovoltaïque. Remarque : cet effet est délicat à utiliser pour réaliser un capteur en revanche il permet de reconnaître le coté P de la photodiode, c’est celui qui possède le potentiel le plus élevé. -Photodiode polarisée en inverse On dit qu’une diode est polarisée en inverse lorsqu’on relie la borne + d’un générateur au coté N de la diode et la borne – au coté P. Lorsqu’on réalise le montage deux précautions sont à prendre : - mettre une résistance de protection en série au cas où on polariserait en direct) - ne pas dépasser la tension inverse maximale (quelques volts). Le montage d’une photodiode en polarisation inverse est donné par la figure 3.

Figure 3

La caractéristique d’une photodiode plongée dans une obscurité totale est schématisée sur la figure 4.

Figure 4

Lorsque la photodiode est éclairée, il apparaît un courant photonique Iph opposé au courant i, ce courant a pour conséquence de décaler la caractéristique vers le bas (cf. figure 4). La résistance r parcourue par un courant i réalise la conversion courant tension, la tension à ses bornes est :

Si on veut que ce courant soit proportionnel à Iph, il faut que la diode reste bloquée. La tension UPN doit rester positive, on en déduit :

La figure 5 représente la caractéristique de la diode pour divers éclairement et diverse résistance (diverses droites de charge).

Figure 5

-Caractéristique de la photodiode polarisée en inverse Le montage exposé précédemment permet d’obtenir un capteur de lumière linéaire, rapide et peu onéreux. C’est donc un capteur couramment utilisé notamment dans les spectrophotomètres visibles.

4. Le phototransistor

Un transistor est constitué de deux jonction PN. Il possède généralement trois pattes :
- la base
- le collecteur
- l’émetteur
Le schéma d’un transistor NPN est donné figure 6.

Figure 6

Ce composant fonctionne à la manière d’un interrupteur, lorsque le courant arrivant sur la base est nul, le transistor est bloqué et aucun courant ne passe du collecteur vers l’émetteur. Dans le cas d’un phototransistor, il n’existe pas de patte sur la base, elle est sensible à la lumière de la même manière que la jonction PN d’une photodiode est sensible à la lumière. Lorsqu’un photon arrive sur la base, il est responsable d’un courant Iph, ce courant « ouvre » l’interrupteur qui est alors parcouru par un courant

Le coefficient ß est un coefficient de multiplication de l’ordre de 100. La présence de ce coefficient améliore grandement la sensibilité du phototransistor, en revanche son temps de réponse est moins bon que celui de la photodiode. L’un des montages les plus simples utilisant un phototransistor est le montage à émetteur commun (émetteur à la masse) représenté à la figure 6.

Figure 7

Lorsque le phototransistor est dans l’obscurité, la tension de sortie Vs est égale à Vcc car le transistor est bloqué. Lorsqu’on éclaire la base du phototransistor, la tension Vs diminue avec l’éclairement et sa valeur est donnée par :

5. La photorésistance

La photorésistance est constitué d’un matériau semi-conducteur homogène, son principe de fonctionnement, nous l’avons trouvé au paragraphe II.2 . Les photons incidents provoque le passage d’un électron de la bande de valence à la bande de conduction, plus il y a d’électrons dans la bande de conduction, plus le matériau devient conducteur et par conséquent lus sa résistance diminue. La résistance varie de manière importante, de quelques MO dans l’obscurité à quelques kO sous éclairement. Un des montages les plus courants utilisant une photorésistance consiste à imposer une tension fixe aux bornes de la résistance et à mesurer le courant I qui traverse le capteur (cf. figure 8).

Figure 8

La photorésistance présente l’inconvénient d’avoir un temps de réponse médiocre, ainsi qu’une non linéarité évidente.

6. Le photomultiplicateur

Un photomultiplicateur est constitué d’une photocathode (mince plaque métallique recouverte d’alcalin) suivie par un dispositif multiplicateur d’électrons, puis par une anode qui collecte les électrons (cf. figure 9).

Figure 9

Les photons incidents frappant la cathode provoquent ainsi l’émission d’électrons par effet photoélectrique. Ces électrons éjectés du matériau sont dirigés vers la première dynode, où ils déclenchent l’émission d’électrons secondaires, à leurs tours accélérés vers la seconde dynode, etc. Le grand intérêt des photomultiplicateur est ce dispositif d’amplification qui permet pour un électron émis par la photocathode d’en recueillir entre 10⁴ et 10⁷ à l’anode ! De plus le photomultiplicateur est un dispositif rapide, le temps de transit des électrons est de l’ordre de la dizaine (au pire de la centaine) de nanoseconde.

III. Les capteurs thermiques

Nous avons vu un large éventail de capteurs photoniques, en ce qui concerne les capteurs thermiques, nous nous contenterons de deux exemples :
- La thermopile
- Le capteur pyroélectrique

1. La thermopile

Le principe des capteurs thermique ayant été exposé au paragraphe I. nous ne nous nous contenterons de le résumer en ces quelques mots : Un rayonnement thermique provoque l’échauffement d’une surface. Dans une thermopile, l’effet qui est utilisé est celui qu’on retrouve dans les thermocouple : lorsqu’on porte les jonctions de deux conducteurs de nature différente reliés entre eux à des températures différentes, il apparaît aux bornes du système une différence de potentiel qui est une fonction de la différence de température (cf. figure 9).

Figure 10

Lorsque la différence de température est faible, la tension de sortie est faible, pour obtenir un signal exploitable, on place une série de thermocouples (en série) dont on relie une jonction à une plaque noircie, les différences de potentiel s’ajoutent alors et on obtient un signal exploitable (cf. figure 10)

Figure 11

La sensibilité d’une thermopile est de l’ordre de 1V/W et son temps de réponse de l’ordre de la seconde ce qui fait de ce capteur un capteur relativement lent. L’avantage de ce type de capteur est une réponse spectrale relativement plate dans le visible.

2. Les capteurs pyroéletriques

Le principe est le même, on retrouve toujours une petite plaque noircie dont la température augmente avec l’éclairement. C’est ce qui se cache sus cette petite plaque qui change ; dans le cas des capteurs pyroéletriques, sous la plaque se trouve un matériau pyroélectrique. Ces matériaux « magiques » possèdent l’étrange propriété de se charger en surface lorsqu’on les chauffe. Les charges qui apparaissent sur les faces opposées du matériau sont de signe opposé et leur nombre est fonction de l’élévation de température. Lorsqu’on place un tel matériau dans un circuit, les charges libres du circuit se déplacent de sorte à compenser l’apparition des charges surfaciques : il apparaît un courant mesurable. La sensibilité de ce type de capteur est de l’ordre de 1kV/W et sa réponse spectrale es elle aussi relativement plate.

IV. Cellules solaires et détecteurs d’images

1. Les cellules solaires

Les cellules solaires ou photopiles permettent de convertir l’énergie du rayonnement solaire et énergie électrique. Elles se présentent sous la forme de plaques de couleur sombre et ne supportent pas d’être polarisées par un générateur extérieur. Les photopiles sont constituées d’une jonction PN identique à celle des photodiodes. Cependant une photodiode est optimisée pour obtenir un courant inverse maximal sous éclairement dans un domaine spectral déterminé. Les photopiles, quant à elles sont optimisées pour fournir la puissance maximale pour u éclairement énergétique dont la distribution spectrale est celle du soleil. Les deux paramètres important pour une photopile sont : - le courant de court circuit I_cc - la tension en circuit ouvert V_co Lorsqu’un photon arrive, il fait passer un électron de la bande de valence à la bande de conduction. Cet électron retombe très rapidement au niveau d’énergie le plus bas de la bande de conduction, il cède alors au cristal une énergie :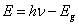

Où Eg est la largeur du GAP. Cet électron est ensuite collecté par e champ électrique qui règne à la jonction ; Il apparaît, en circuit ouvert, une tension aux bornes de la cellule de l’ordre de . Quant au courant de court circuit, c’est tout simplement le produit du nombre de photon par la charge élémentaire q (chaque photon crée un électron. Pour que tout photon du rayonnement solaire provoque l’apparition d’un électron il faut adapter la largeur du GAP. En effet, seul les photons d’énergie supérieure au GAP pourront être captés. Le spectre du soleil s’étendant de 300nm à 2,5µm, un GAP de l’ordre de 0,5eV devrait faire l’affaire. En réalité un compromis est nécessaire pour optimiser la puissance et le GAP est de l’ordre de 1 à 2eV.

2. Les détecteurs d’image

Il est parfois utile d’étudier non plus le flux reçu en une petite surface d’un plan mais la répartition énergétique dans tout un plan, pour réaliser cette tache, nous devons faire appel aux détecteurs d’image. Le premier détecteur d’image est le film argentique, les progrès en ont fait le détecteur d’image le plus performant en terme de résolution spatiale. Cependant, l’instrumentation moderne nécessite le plus souvent des données électriques, on a donc développée des capteurs d’images électriques. Nous nous restreignons ici au cas des barrettes de photodiodes dont le fonctionnement est relativement simple. Il s’agit de circuits intégrés comportant une rangée de photodiodes auxquelles sont asociées autant de transistors (cf. figure 11).

Figure 12

Initialement les transistors sont passant et les photodiodes polarisées en inverse. Lors de l’exposition, les transistors sont bloquées, les photons incidents créent des paires électrons trous qui diminuent progressivement la polarisation des diodes (on se rapproche de plus en plus de la situation diode passante). Ensuite vient la phase de lecture. Pour lire le flux reçu par chaque photodiode, on ouvre le transistor correspondant, la photodiode se repolarise alors en empruntant des charges au circuit extérieur : c’est cette charge qui est mesurée via le potentiel au point S. en opérant ainsi pour chaque photodiode, on obtient la répartition de l’énergie lumineuse sur toute la surface.

I. Le cadre de l’optique géométrique

1. Description géométrique de la lumière

Plaçons une source ponctuelle derrière un écran percé d’un trou circulaire. Après l’écran, lorsqu’on déplace une feuille de papier, on observe un cercle qui devient de plus en plus gros lorsqu’on s’éloigne de l’écran percé. La lumière s’échappe ainsi par l’ouverture en suivant un cône de lumière : on parle alors de faisceau lumineux issu de l’ouverture. En s’échappant de l’ouverture, il semble alors que la lumière se propage en ligne droite. Cette propagation rectiligne se retrouve encore lorsqu’on observe la propagation de la lumière issue d’un laser. Dans un milieu homogène et isotrope , la lumière se propage en ligne droite. A la fin d’une averse, on voit souvent le soleil « percer les nuages », on voit alors les rayons du soleil descendre jusqu’au sol et réchauffer la Terre. Et c’est ainsi que l’on décrit la lumière en optique géométrique : nous dirons dans ce chapitre que la lumière est constituée d’un ensemble de lignes droites appelées « rayons lumineux ». Un faisceau lumineux est donc un ensemble de rayons lumineux rectilignes. L’objet de l’optique géométrique est de décrire la propagation de ces rayons lumineux.

2. Principes fondamentaux

Reprenons l’expérience d’une source de lumière placée derrière un diaphragme. Au départ, le diaphragme possède une large ouverture, la base du cône est alors large et de nombreux rayons passent à travers l’ouverture. On rétrécit ensuite cette ouverture, certains rayons qui passaient dans le cas précédent sont maintenant arrêtés. Ceux qui passent encore n’en son absolument pas perturbé : les rayons lumineux sont indépendant les uns des autres. Reprenons maintenant une source laser, on place le laser en un point A et en B on place un miroir. Pour aller de A vers B, la lumière se propage en ligne droite, lorsqu’elle arrive en B, elle se réfléchit et repart vers A en empruntant le même chemin. Ce que nous avons remarqué sur cet exemple simple, est une réalité générale : si pour aller d’un point A vers un point B, la lumière emprunte un chemin, alors elle empruntera le même chemin pour aller de B vers A.

II. Les lois de Snell-Descartes

1. Indice optique d’un milieu

Le but de l’optique géométrique, est de décrire le parcours de la lumière dans la matière en termes de rayons lumineux. Pour atteindre cet objectif, la notion essentielle est la notion d’indice optique. L’indice optique d’un milieu est caractéristique de la vitesse de propagation de la lumière dans ce milieu. Dans le vide, la vitesse de propagation de la lumière est c, dans un milieu d’indice n, la lumière se déplacera à la vitesse . L’indice optique est caractéristique du milieu. Durant le même temps, la lumière parcourt une distance plus grande dans le vide que dans un milieu d’indice n. Le chemin optique est la distance que la lumière aurait parcouru dans le vide en le même temps qu’elle met pour aller d’un point A à un point B dans un milieu d’indice n. Dans le vide,la vitesse de la lumière étant c, elle parcourt la distance :

2. Lois de Snell-Descartes

L’optique géométrique permet de décrire deux phénomènes qui interviennent dans la propagation de la lumière :
- la réflexion
- la réfraction
Ces phénomènes interviennent lorsque la lumière arrive à l’interface de deux milieux (dioptre) et sont décrits par les lois de Snell-Descartes . Conventions Avant d’énoncer les lois de Descartes, attachons nous un instant à mémoriser quelques conventions importantes en optique géométrique. La plupart du temps, nous aurons besoin de mesurer des angles, c’est là la première convention : Les angles sont mesurés à partir de la normale aux surfaces 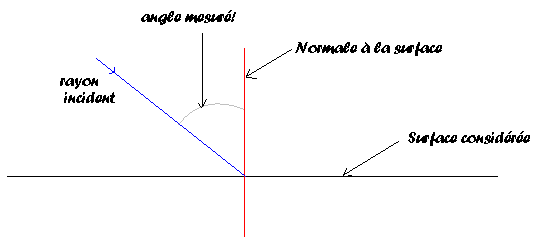De manière générale, on considère la lumière se déplaçant de la gauche vers la droite et on établit des distances algébriques, c’est à dire qu’on pourra avoir des signes devant une distance. Lois de la réflexion et de la réfraction Soit le schéma suivant : 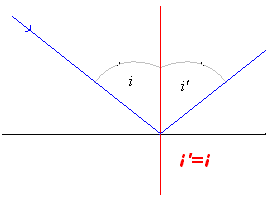Si un rayon lumineux arrive sur une surface réfléchissante en formant un angle i avec la normale à cette surface, il sera réfléchi suivant le même angle i et dans le même plan que le rayon incident ! On retiendra les lois de la réflexion sous la forme :
- angle d’incidence = angle de réflexion
- plan d’incidence = plan de réflexion
Il y a réfraction lorsque le rayon lumineux passe d’un milieu 1 à un milieu 2 avec un changement de trajectoire. La surface séparant ces deux milieux est appelée dioptre. Dioptre : Surface transparente séparant deux milieux homogènes et transparent d’indice n et n’. Considérons un rayon lumineux arrivant sur un dioptre avec une incidence i : La loi de la réfraction va nous permettre de prévoir l’angle que ce rayon formera avec la normale après la traversée du dioptre. On considère que le milieu 1 possède un indice optique n et que le milieu 2 possède un indice n’. Les lois de la réfraction sont les suivantes :
-
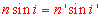
- plan réfracté = plan incident
Définition :
- si n' est supérieur à n alors que le milieu 2 est plus réfringent que le milieu 1
- si n' est inférieur à n alors le milieu 2 est moins réfringent que le milieu 1

3. Construction de Descartes

Le rayon incident arrive sur le dioptre en I , si on trace un cercle de rayon n1 et un autre de rayon n2. Le rayon incident coupe le cercle de rayon n1 en K. La perpendiculaire au dioptre passant par K coupe le cercle de rayon n2 en R’. Le segment IR’ indique alors la direction du rayon réfléchi !

4. Angle limite de réfraction

On considère le dioptre séparant un milieu d’indice n et un milieu d’indice n’ tels que n , en revanche après le dioptre il existe une valeur limite de l’angle de réfraction : c’est l’angle limite de réfraction . Exprimons cet angle limite de réfraction : si on considère une incidence de , la loi de la réfraction nous donne : Remarque : on fera bien attention au fait que n est inférieur à n’ sinon cela signifierai un sinus supérieur à 1 : impossible !!

5. Réflexion totale

Inversons le problème précédent et plaçons cette fois-ci la source lumineuse dans le milieu d’indice n’>n. l’angle d’incidence peut toujours varier entre 0 et 90°, et la loi de Descartes est toujours valable : En revanche il existe un angle limite au-delà duquel on n’observe plus de rayon réfracté, toute la lumière incidente est alors réfléchie, c’est le phénomène de réflexion totale. Cet angle est défini par : Lorsque i’est supérieur à il ya réflexion totale.

6. Applications

La fibre optique Le phénomène de réflexion totale est à la base du fonctionnement des fibres optiques. Une fibre optique à saut d’indice est constituée d’un cœur et d’une gaine. L’indice du cœur est plus élevé que celui de la gaine. Lorsqu’un rayon provenant du cœur de la fibre optique arrive sur le dioptre cœur/gaine sous un angle supérieur à l’angle limite de réfraction, il y a réflexion totale et la lumière se propage dans la fibre. Le réfractomètre Le réfractomètre permet la mesure de l’indice optique d’une substance. Nous allons nous restreindre ici, comme c’est généralement le cas en chimie organique, à la mesure de l’indice optique d’un liquide. La détermination de l’indice optique permet :
- d’identifier la substance
- de contrôler la pureté d’un produit
Un réfractomètre portatif peut être schématisé par la figure suivante. La substance d’indice ns à analyser est déposée sur la surface d’un prisme d’indice np proche de 1,8. Elle est éclairée via un couvercle diffusant la lumière ce qui permet d’obtenir des angles d’incidence variant de 0 à 90°. L’indice de la substance étant plus faible que celui du prisme, on peut assister au phénomène de réfraction limite, c'est-à-dire que tous les rayons arrivant avec un angle d’incidence proche de 90° ressortent du prisme avec un angle limite ilim défini par : Tous les points de la surface du prisme étant éclairés par des rayons dont l’incidence varie entre 0 et 90°, on observera un ensemble de rayons émergents du prisme mais pour lesquels l’angle d’émergence possède une valeur maximale : celle qui correspond à ilim. En plaçant une lentille après le prisme, tous les rayons de même inclinaison vont converger au même point du plan focal image de cette lentille. Les rayons émergents avec l’angle limite de réfraction convergent en un point du plan focal de la lentille définissant la limite entre une zone éclairée et une zone sombre. On place alors dans ce plan une échelle graduée et transparente, puis on forme l’image de ce plan par une lentille L2 (l’oculaire). En regardant à travers l’oculaire, on voit une zone sombre et un zone éclairée et on peut ainsi lire la valeur de l’indice optique de la substance

III. Généralités sur la formation des images

1. Le but d’un instrument d’optique

Un instrument d’optique a pour but de donner d’un objet quelconque une image la plus ressemblante possible. Dans le cas idéal, on cherche donc à réaliser la correspondance entre un point de l’objet et un point de l’image. Nous verrons que cette correspondance n’est que trop rarement réalisable.

2. Définitions

Stigmatisme : On dit qu’il y a stigmatisme parfait lorsque l’image d’un point est un point. Lorsque l’image d’un point est une toute petite tache, on dit qu’il y a stigmatisme approché. Axe optique : L’axe optique est l’axe de révolution du système optique (instrument). Aplanétisme : On dit qu’il y a aplanétisme lorsque deux points, A et B, de l’objet appartenant à un plan perpendiculaire à l’axe optique fournissent des images A’ et B’ appartenant à un plan perpendiculaire à l’axe optique. Source primaire : une source primaire est un objet qui produit de la lumière (exemples : soleil, ampoule) Source secondaire : c’est un objet qui reçoit de la lumière d’une source primaire et qui la réfléchit en partie ou intégralement (arbres, tables…).

3. Images et objets

Un objet est une source primaire ou secondaire qui envoient des rayons lumineux sur le système optique ; celui-ci les dévient et des rayons lumineux ressortent de ce système optique : l’image est le point de convergence de ces rayons lumineux. Un objet est dit réel si les rayons qui arrivent sur le système optique proviennent directement de lui. Dans le cas où ce sont les prolongements des rayons qui arrivent sur le système optique, l’objet est dit virtuel. Une image est dite réelle si les rayons qui émergent du système optique passent effectivement par elle. Dans le cas où se sont les prolongements des rayons émergents qui passent par l’image, elle est dite virtuelle. Objet Réel Objet virtuel Image réelle Image virtuelle Pour résumer :

IV. Les lentilles minces

1. Notion de lentilles minces

La lentille mince est le système optique le plus simple. Elle est formée de l’association de deux dioptres sphériques dont les sommets sont pratiquement confondus au même point.

Nous n’étudierons dans ce cours que les lentilles minces, c'est-à-dire des lentilles pour lesquelles la distance S1S2 est très petite devant le rayon de courbure des dioptres. On assimile alors la lentille à son plan : c’est le plan perpendiculaire à l’axe optique en O. La représentation d’une lentille mince (convergente) est la suivante :

La plupart des lentilles sont réalisées en verre d’indice optique proche de 1,5.

2. Les conditions de Gauss

Les lentilles ne sont pas planes et leur indice optique est fonction de la longueur d’onde , ces deux constatations font de l’étude des lentilles une chose délicates. Cependant il est possible de simplifier cette étude en se plaçant dans les conditions de l’approximation de Gauss : - les rayons incidents dont faiblement inclinés sur l’axe optique - les rayons sont proches de l’axe optique Dans ces conditions, la majeure partie des défauts de la lentille peut être négligée. La recherche de ces conditions est donc une chose assez fréquente lorsqu’on veut réaliser l’image d’un objet : et c’est l’objet de ce cours !

3. Foyers et distance focale

Une lentille est caractérisée par la position de deux points : - le foyer principal objet F - le foyer principal image F’ Nous admettrons que ces deux points sont symétriques l’un de l’autre par rapport à O. On définit la distance focale d’une lentille par . Si la lentille est dite convergente. Si la lentille est dite divergente.

4. Construction d’une image

Trois rayons permettent de construire l’image d’un objet à travers une lentille. Rayons parallèles à l’axe optique Un rayon arrivant parallèle à l’axe optique ressort en passant par le foyer principal image

Rayons passant par le foyer principal objet Un rayon qui passe par le foyer principal objet ressort parallèle à l’axe optique

Rayon passant par le centre Un rayon passant par le centre optique O n’est pas dévié.

5. Relation de conjugaison

Puisqu’il faut parfois faire des calculs, on cherche une relation entre objet et image, cette relation porte le nom de relation de conjugaison.

Etude des triangles ABF et FOJ

On peut y appliquer la relation de Thalès.

Or

et

On en déduit

(1)

Etude des triangles A’B’F’ et F’OI

Or

et

On en déduit

(2)

En égalant les deux expressions :

(3)

Les expressions que nous venons d’établir portent le nom de relation de Newton. C’est à partir de la dernière expression qu’on démontre la relation de conjugaison.

6. Grandissement

Le grandissement d’un système optique est donnée par

En utilisant la deuxième relation de Newton

Or en utilisant la formule de conjugaison, on obtient :

7. Objet à l’infini

On peut former à l’aide d’une lentille convergente l’image d’un objet à l’infini… mais l’infini, peut –on le voir ?? Nous allons voir que l’infini peut être bien plus proche qu’on se l’imagine. Formons à l’aide d’une lentille convergente de distance focale f’=1m, l’image d’une tour AB de hauteur h=30m située à 3km de la lentille. La relation de conjugaison s’écrit alors :

On obtient L’image se forme dans le plan focal image !! L’immeuble est donc situé à l’infini ! L’autre problème qui se pose est celui de la taille de l’image. La plupart du temps, on souhaite obtenir une image plus grande que celle qu’on observe à l’œil nu. Pour préciser cette notion, on doit introduit la notion de diamètre apparent. Un objet de hauteur AB perpendiculaire à l’axe optique et à une distance D de notre œil est vu sous un angle

En utilisant le fait que le rayon passant par le centre n’est pas dévié, on peut écrire

Soit

Plus la distance focale est grande, plus l’image sera grande !!!

V. L’œoeil

1. Description

Le plus répandu des capteurs optiques est l’œil, c’est lui qui nous permet de voir le monde qui nous entoure. L’œil est un système optique complexe :

Les rayons lumineux entrent dans l’œil en passant à travers la cornée, l’humeur vitreuse et sont limités par la pupille. Puis le cristallin en donne une image qui se forme sur la rétine. Celle-ci est constituée de capteurs photosensibles qui transforment l’énergie lumineuse en impulsion électrique, c’est cette impulsion électrique qui est transmise au cerveau par le biais du nerf optique.

2. Modélisation

Ce capteur bien complexe peut être modélisé en travaux pratique à partir d’éléments simples :. Le rôle de la pupille est joué par un diaphragme à ouverture variable qui permet à l’œil de travailler dans les conditions de Gauss. Le cristallin est modélisé par une lentille. En réalité le cristallin est une lentille dont la distance focale peut varier sous l’action des muscles de l’œil. La rétine peut se modéliser par un écran dépoli.

3. Les problèmes de vue

Un œil normal est un œil qui voit distinctement des objets à l’infini. Dans cette configuration l’œil travaille sans fatigue car les muscles de l’œil sont décontractés, la distance cristallin rétine est alors égale à la distance focale du cristallin ( 25mm). Le cristallin peut ajuster sa distance focale mais pas de manière indéfinie, il existe une limite à cette accommodation. Le punctum proximum en est une manifestation : il s’agit de la distance la plus faible de vision distincte. Pour un œil normal il est situé à 25cm de l’œil. Le plus grande distance visible par l’œil correspond à la position du punctum remotum, pour l’œil normal il est à l’infini. Un œil est dit myope si le cristallin est trop convergent, son punctum remotum est à distance finie et le punctum proximum est plus près de l’œil. On corrige ce défaut par des lentilles divergentes. Un œil est dit hypermétrope si le cristallin n’est pas assez convergent, le punctum remotum se situe alors plus loin de l’œil. On corrige ce défaut par des lentilles convergentes. Un œil est dit astigmate s’il ne possède pas la symétrie de révolution. On corrige ce défaut par des lentilles cylindriques. Avec l’âge, la capacité d’accommodation de l’œil diminue et le Punctum Proximum s’éloigne : c’est la presbytie.

VI. Instruments d’optique

1. Généralités

Un instrument d’optique est destiné à améliorer la vision que nous pouvons avoir d’un objet à l’œil nu. Il s’agit souvent d’examiner des détails invisibles à l’œil nu : c’est le cas de la loupe, du microscope, de la lunette astronomique et des instruments de projection. Les instruments d’optiques sont nombreux, le but, ici, n’est pas d’en faire une description systématique mais de donner les principes généraux des instruments les plus utilisés (surtout en chimie). D’une manière générale, les instruments d’optiques doivent permettre à l’utilisateur d’observer les détails voulus sans se fatiguer c'est-à-dire sans que l’œil ne fatigue. L’œil ne doit pas accommoder en regardant à travers un instrument : l’image doit donc se former à l’infini.

2. Le collimateur

Le collimateur est un instrument de laboratoire destiné à procurer l’équivalent d’un objet à l’infini. Il se compose d’un premier objet (trou, réticule, mire) éclairé par une source lumineuse et situé dans le plan focal objet d’une lentille convergente. Cette lentille donne de cet objet une image à l’infini qui pourra elle-même servir d’objet pour un autre dispositif.

3. L’objectif

C’est le premier élément d’un instrument d’optique, c’est lui qui reçoit les rayons lumineux issus de l’objet à analyser. Il forme une image intermédiaire de l’objet qui sert ensuite d’objet à l’oculaire par exemple.

4. L’oculaire

Un oculaire est une lentille mince (ou le plus souvent un doublet de lentilles). L’oculaire est en général la dernière pièce d’un instrument d’optique, c’est lui qui permet de voir dans de bonnes conditions. L’oculaire sert donc à voir l’image intermédiaire qui est formé par un système optique.

I. La lumière

1. Une onde électromagnétique

La lumière est une onde électromagnétique, elle se compose d’un champ électrique et d’un champ magnétique évoluant dans le temps. Cette onde est une onde transversale, de ce fait le vecteur champ électrique et champ magnétique sont perpendiculaires à la direction de propagation. Cette description du champ magnétique due à Maxwell apporte deux éléments nouveaux pour vous et qui méritent toute notre attention : - La lumière est constituée de vecteurs, or ces objets mathématiques ont certaines particularités qui vont se répercuter sur les propriétés de la lumière - La lumière est une onde tout comme le son ou les rides à la surface de l’eau, elle est régie par les mêmes lois et nous devrions observer les mêmes phénomènes tels que la diffraction. C’est donc sur ces deux aspects que nous allons nous attarder dans ce chapitre. Nous poserons tout de même une simplification, la lumière qui nous entoure est une superposition complexe de longueur d’onde et de surface d’onde sphériques et planes mais nous nous limiterons à l’étude d’onde plane monochromatique. Cette simplification se justifie parle théorème de Fourier qui postule que toute onde peut être écrite comme une somme continue d’onde plane monochromatique, en étudier une permet donc de les étudier toutes !

2. Les « grains » de lumière

Une autre théorie de la lumière postule qu’elle est constituée de particules sans masse transportant avec elles une énergie fonction de la longueur d’onde associée à la lumière : les photons. Dans cette représentation la lumière interagit avec la matière au travers de chocs entre particules (effet Compton, photoélectrique). Elle est très pratique pour expliquer le fonctionnement de certains capteurs de flux lumineux comme nous allons le voir dans un prochain chapitre mais pour expliquer la notion de polarisation ou de diffraction à partir de cette vision des choses, il faut faire appel à la mécanique quantique, et cela dépasse de loin le cadre de ce cours…

II. Polarisation : Conséquence du caractère vectoriel de la lumière

1. Définition

Intéressons nous au cas simple d’une onde plane monochromatique se propageant suivant l’axe des x. La description de la lumière passe alors par la description du champ électrique, le champ magnétique se déduisant de celui-ci . Dans le cas le plus général, le champ électrique possède une composante suivant l’axe Oy et une composante suivant l’axe Oz. On peut donc écrire : Le champ électrique est constitué de deux vibrations perpendiculaires qui oscillent autour de 0 avec un déphasage. Etudier la polarisation de la lumière c’est étudier l’évolution du vecteur champ électrique au cours du temps. Cette évolution est fonction du déphasage entre les deux composantes du vecteur champ électrique. Remarque : Le plan de polarisation est, dans un milieu isotrope, le plan défini par la direction de propagation du rayon lumineux (donc ) et la direction du champ électrique.

2. Les états de polarisation

Comme nous l’avons dit précédemment, l’état de polarisation de l’onde plane monochromatique que nous sommes en train de décrire est fonction du déphasage entre les composantes selon Oz et Oy du vecteur champ électrique. Nous allons donc étudier certains cas particuliers. Les composantes sont en phase Lorsque les deux vibrations sont en phase, le vecteur résultant garde une direction fixe suivant laquelle il oscille : la polarisation est alors rectiligne. 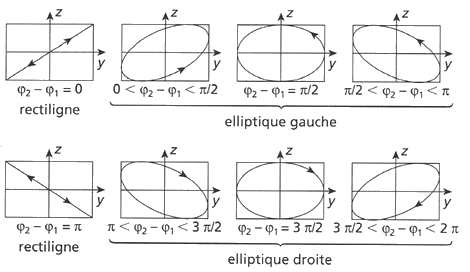Les composantes sont en opposition de phase Lorsque les vibrations sont en opposition de phase, le résultat est le même, le vecteur garde une direction fixe (perpendiculaire à la précédente) : la polarisation est encore rectiligne Les composantes sont déphasées Lorsque le déphasage est quelconque, le vecteur décrit une ellipse : la polarisation est dite elliptique. Lorsque cette ellipse est parcourue dans le sens trigonométrique : la polarisation est dite gauche. Lorsqu’elle est parcourue dans le sens des aiguilles d’une montre, la polarisation est dite droite. On peut résumer ces résultats à l’aide du tableau de la figure 1.

Figure 1 A chaque fois qu’une lumière est dans l’un des états décrits par la figure 1, on dit qu’elle est polarisée, autrement elle est non polarisée ou partiellement polarisée.

3. Lumière naturelle et Polarisation de la lumière

La lumière naturelle, elle qui est produite par une ampoule ou celle qui provient du soleil n’est en général pas polarisée. Ceci s’explique toujours à l’aide du déphasage , celui-ci est parfaitement aléatoire dans le cas de la lumière naturelle, de ce fait la lumière naturelle est une superposition de tous les états de polarisations que nous avons décrites précédemment : on dit qu’elle n’est pas polarisée. La lumière naturelle n’est pas polarisée. La lumière naturelle par excellence est celle provenant du soleil, celle là n’est absolument pas polarisée, en revanche la lumière qui nous parvient à chaque instant n’est plus tout à fait naturelle, elle a été polarisée. Un certain nombre de phénomènes sont capables de polariser la lumière naturelle, par exemple, lorsque la lumière se réfléchit sur une vitre, elle se polarise partiellement. Lorsqu’elle traverse des particules en suspension, elle se polarise un peu aussi. Mais ces phénomènes n’aboutissent que très rarement à la polarisation complète de la lumière et elle ets finalement partiellement polarisée. Lorsque la lumière est un mélange de lumière naturelle et de lumière polarisée, on dit qu’elle est partiellement polarisée. Imaginons maintenant que nous parvenions à faire subir de multiples réflexions à un faisceau de lumière naturelle peut-être finirait-elle par être entièrement polarisée ? Ce passage d’une lumière non polarisée ou partiellement polarisée à une lumière ayant une polarisation particulière est assurée par un polariseur.

4. Entre polariseur et analyseur

Les polariseurs les plus courants sont constitués de polymères alignés les uns à coté des autres dans une direction donnée. Sur ces polymères sont rattachées des molécules de colorant capables d’absorber la lumière. L’absorption de la lumière ne se fait que dans une direction donnée si bien que ces polariseurs sont capables d’éteindre une des composantes du champ électrique (suivant Oy ou suivant Ox). En conclusion un polariseur transforme une lumière de polarisation quelconque en lumière de polarisation rectiligne. C’est donc un moyen « artificiel » de produire de la lumière polarisée.

Figure 2 Si on réalise le montage de la figure 2, on ne constate à l’œil nu aucun changement des propriétés du faisceau lumineux, comment peut-on déceler la polarisation de la lumière ? Pour observer un changement, il faut placer sur le trajet du faisceau un analyseur. Cet analyseur est en tout point identique au polariseur, lorsqu’on fait varier son orientation on constate que l’intensité du faisceau émergent varie. De plus il existe une position particulière où on réalise l’extinction du faisceau. Il existe une relation reliant l’intensité lumineuse incidente sur un analyseur et l’intensité qui en émerge ; cette relation porte le nom de loi de Malus :

Où est l’angle entre la direction du polariseur et celle de l’analyseur

5. Substance optiquement active

La polarisation est une caractéristique peu connue de la lumière et pour cause, elle est invariante lors de la traversée de la plupart des milieux ; la plupart mais pas tous… Certaines substances sont capables de faire tourner la direction de polarisation du champ électrique (ou plus généralement le plan de polarisation de la lumière): ce sont les substances optiquement actives. Chaque substance est caractérisée par son pouvoir rotatoire spécifique, il est caractéristique de la capacité d’une substance à faire tourner la direction de polarisation de la lumière. Le pouvoir rotatoire spécifique représente l’angle dont tourne la direction de polarisation du champ après la traversée de 1dm de solution optiquement active de concentration 1g/L. Au même titre que le point d’ébullition ou l’indice optique le pouvoir rotatoire spécifique constitue une carte d’identité de la substance. Après la traversée d’une distance l de solution de concentration c, langle dont a tourné la direction de polarisation du vecteur est donné par la loi de Biot :

• () pouvoir rotatoire spécifique
• pouvoir rotatoire de la solution
• l longueur de la cuve en dm
• c concentration massique en g/L

Si la substance a fait tourner le champ électrique vers la droite elle est dextrogyre, au contraire si le cham électrique a tourné vers la gauche elle est dite lévogyre. Pour interpréter l’activité optique d’une substance, il faut savoir que toute polarisation rectiligne peut s’écrire comme la somme de deux polarisations circulaires : une circulaire droite et une circulaire gauche. Lorsque l’onde pénètre dans le milieu optiquement actif, elle se décompose en ses deux composantes circulaires. A chacune de ces composantes est associé un indice optique qui lui est propre :

• nD pour la polarisation circulaire droite
• ng pour la polarisation circulaire gauche

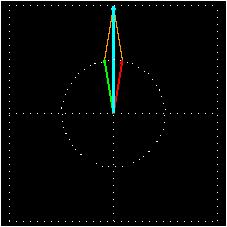
Le chemin optique parcouru par chaque composante est donc différent, il en résulte un déphasage à la sortie et une rotation du vecteur électrique. Cette activité optique ne peut être le fruit que d’une brisure de la symétrie droite-gauche, par conséquent une substance optiquement active est une substance chirale. A titre d’exemples voici le pouvoir rotatoire spécifique de quelques substances

6. Le polarimètre de Laurent

La loi de Biot est très intéressante pour un chimiste, en effet moyennant la connaissance du pouvoir rotatoire spécifique d’une substance, la mesure de l’angle dont a tourné la direction de polarisation du champ électrique après la traversée d’une cuve de longueur connue permet de déterminer la concentration. Le tout c’est de mesurer l’angle a !! D’un point de vue purement théorique il suffirait de réaliser le montage suivant :

Initialement dans la cuve, on ne met rien lorsque la direction du polariseur forme un angle de 90° (on dit qu’ils sot croisés) avec celle de l’analyseur le faisceau lumineux est éteint. Lorsqu’on verse la substance à l’intérieur de la cuve, on constate une réapparition du faisceau et il faut tourner l’analyseur pour réobtenir l’extinction : l’angle dont on a tourné l’analyseur correspond au pouvoir rotatoire de l’échantillon. Cette méthode si simple n’est pourtant pas utilisée dans la pratique car très peu précise. En effet il est très difficile de repérer l’extinction totale d’un faisceau. L’œil est très peu apte à déceler de faible variation de luminosité autour de l’extinction, il est en revanche bien plus apte à comparer deux niveau de luminosité : c’est ce point qui est mis à profit dans le polarimètre de Laurent. Un polarimètre de Laurent est un tube cylindrique contenant les éléments suivants :

• Une lampe spectrale au sodium pour source lumineuse
• Un polariseur qui produit une lumière polarisée rectilignement et dont la direction de polarisation fait un angle beta avec la verticale.
• Une lame demi-onde qui occupe la partie inférieure du cylindre et qui est capable de transformer une polarisation rectiligne en une autre polarisation rectiligne symétrique par rapport à la première
• Une cuve à échantillon dont la longueur est généralement de 1dm
• Un analyseur
Commençons par voir ce qui se passe si il n’ya a pas de cuve à échantillon. Tout d’abord, le polariseur produit une lumière polarisée rectilignement et formant un angle ß avec la verticale (rouge). Vient ensuite la lame demi-onde qui transforme la partie inférieure du faisceau lumineux en une lumière polarisée rectilignement et dont la direction de polarisation forme un angle –ß avec la verticale (bleue). Si on veut obtenir le même éclairement sur l’écran il faut que les angles entre l’analyseur et chacune des directions de polarisation soient les mêmes : l’analyseur peut être vertical ou horizontal (l’angle entre la direction de l’analyseur et la direction de polarisation de la lumière n’ayant pas traversé la lame retard (rouge) doit être égal à l’angle entre la direction de l’analyseur et la direction de polarisation de la lumière ayant traversée la lame retard (bleue)). Si cet angle est petit (analyseur en position 1, vertical) comme représenté sur le schéma ci-dessous, le cosinus sera grand et l’intensité lumineuse grande (Loi de Malus) et ce n’est pas souhaitable pour des raisons de précisions identiques à celles qui nous ont amenées au polarimètre de Laurent.



En revanche si cet angle est grand (analyseur en position 2, horizontal), le cosinus sera petit et l’intensité lumineuse faible et identique dans les deux parties.



Que se passe-t-il maintenant lorsqu’on introduit un échantillon optiquement actif dans le polarimètre ? L’échantillon est placé après la lame demi onde et occupe tout le cylindre si bien que quelque soit la polarisation du faisceau la direction de polarisation tournera du même angle a : Tout se passe donc comme si les deux direction de polarisation (celle du haut et celle du bas) bascule d’un angle a. Pour rétablir l’équipénombre, il faudra par conséquent tourner l’analyseur du même angle et dans le même sens comme indiqué par la figure ci-dessous.



Remarque : La fonction cosinus étant définie modulo 2p, on obtiendrait le même éclairement en tournant l’analyseur des angles 180+ et 360+ !

III. Nature ondulatoire de la lumière : interférence et diffraction

1. Résultats expérimentaux

Lorsqu’on s’arrête à une station essence pour faire le plein, il n’est pas rare de voir sur le sol des taches de carburant. Lorsque la lumière du soleil vient frapper cette pollution, il apparait alors à la surface des taches de gasoil des couleurs, comme sur un arc en ciel. Ce phénomène est due au caractère ondulatoire de la lumière et porte le nom d’interférence. L’ensemble des couleurs qu’on observe dans ce phénomène est due à la lumière du soleil. On peut réaliser des expériences d’interférence à l’aide de source monochromatique et on aboutit alors à un résultat stupéfiant : L’addition de deux sources lumineuses peut aboutir à des zones d’ombres come le montre la figure ci-dessous.



Et c’est cette apparente contradiction que nous allons tenter d’expliquer en premier lieu.

2. Notion d’interférence

Commençons par étudier le cas le plus simple et considérons deux sources ponctuelles monochromatiques fournissant une onde lumineuse de même polarisation et de même pulsation. Le champ électrique associé à chaque source s’écrit donc au point M de la manière suivante : - pour S1



- pour S2



Les vecteurs étant colinéaires nous pourrons par la suite les omettre. Au point M, il ya une vibration qui arrive et elle peut s’écrire :

(1)

Or :

(2)

D’où :

(3)

Cette amplitude résulte de la somme des amplitudes des deux ondes émises par S1 et S2 :



Il vient alors en utilisant (2):



Par identification, on obtient :

(4)

Lorsque les amplitudes de sonde s’additionnent de la sorte, on dit qu’il ya interférence mais revenons à notre apparente contradiction ; ce que nous voyons ce n’est pas l’amplitude du champ électrique mais l’intensité lumineuse (l’énergie).Or on montre que l’intensité lumineuse au point M est proportionnelle à la norme du vecteur champ électrique au carré, c'est-à-dire :



Exprimons donc cette quantité en utilisant (4) :



Finalement l’intensité lumineuse au point M s’écrit :



La dernière relation que nous venons d’écrire comporte un terme dit terme d’interférences, c’est :



Lorsque ce terme n’est pas nul, l’intensité au point M n’est pas la somme des intensités de chacune des ondes émises par les sources S1 et S2. L’étude des interférences s’appuie donc sur l’étude de ce terme. Il convient par conséquent de s’attarder un peu sur cette expression. Le terme crucial dans cette expression est le déphasage développons ce terme. Nous avons défini la phase de l’onde en un point M par :



Or



On en déduit :



Et la vitesse de la lumière dans un milieu d’indice n est , il vient donc :



Soit finalement :



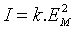
La phase de l’onde en un point M est égale à la phase à l’origine plus fois le chemin optique. Ce résultat peut nous aider à expliciter le terme d’interférences . Il intervient dans ce terme une différence de phase , on peut exprimer cette différence de phase en fonction du chemin optique :



En supposant que les phases à l’origine soient identiques, on obtient :



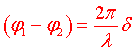
Où est la différence de marche entre les rayons issus de S1 et ceux issu de S2. L’intensité résultante de l’interférence de sources ponctuelles monochromatiques s’écrira finalement :



3. Condition d’obtention des interférences

Si deux sources ponctuelles monochromatique et de même polarisation sont placées en deux points distinct de l’espace S1 et S2, l’intensité lumineuse en un point M est donnée par :



On observe donc en ce point des interférences. Examinons d’un peu plus près cette affirmation. Dans une pièce, il n’est pas rare que deux ampoules soient allumées, pourtant on n’observe aucun phénomène d’interférences. Peut-être me direz vous que ce ne sont pas des sources monochromatiques, qu’à cela ne tienne ! Plaçons devant ces ampoules un filtre : toujours pas d’interférences ! Alors peut être ces ampoules ne sont-elles pas des sources ponctuelles. On placera donc un diaphragme…mais toujours pas d’interférences. Dernier essai, la lumière n’est pas polarisée, plaçons donc devant ces sources ponctuelles des polariseurs …et non toujours pas d’interférences. La formule que nous avons trouvée serait-elle donc fausse ? Pour y répondre, il suffit d’observer les étapes qui nous y ont conduit, quelques lignes avant d’aboutir à cette formule finale, vous trouverez la phrase : « En supposant que les phases à l’origine soient identiques ». Cette phrase est la clé de toute notre recherche. Ce qui fait briller le filament d’une ampoule c’est l’émission d’un train d’onde par les atomes du filament lors de leur passage d’un état excité à un état plus stable, ce n’est pas une émission continue car un train d’onde à l’allure suivante :



Ce que l’on observe en M c’est la valeur moyenne temporelle du cos mais les trains d’ondes ayant des phases à l’origine totalement aléatoire cette moyenne est nulle ! Ces quelques phrases suffisent à expliquer l’impossibilité d’obtenir des interférences avec les ampoules d’une salle. En conclusion, il faudra donc retenir qu’avant de transformer une salle de séjour en véritable laboratoire scientifique il vaut peut être mieux se pencher sur les hypothèses qui nous ont permis d’obtenir les relations qu’on cherche à appliquer. Revenons maintenant à nos interférences. Comment peut-on obtenir des interférences puisqu’on ne peut pas utiliser deux sources distinctes ? La réponse est dans la question : il faut utiliser une seule source et créer à partir de cette source deux sources secondaires, ces sources secondaires sont dites cohérentes.

4. Dispositifs interférentiels

Pour obtenir des interférences, il faut à partir d’une source créer deux sources secondaires distinctes. Il existe deux possibilités pour créer ces sources : - la division d’amplitude, qui consiste à séparer l’énergie lumineuse issue de la source primaire en deux faisceaux d’énergie égale. Cette division est la plupart du temps réalisé à l’aide d’une lame semi transparente. - la division du front d’onde qui consiste tout simplement à diviser une surface d’onde, pour cela on place devant la source un objet percé de deux très petites ouvertures, ces ouvertures deviennent les sources secondaires.

5. Interféromètre de Michelson

Description Le dispositif à division d’amplitude le plus courant est l’interféromètre de Michelson. Nous n’étudierons ici qu’un cas particulier d’utilisation de cet interféromètre, celui qui est utilisé dans les spectroscopes à transformée de Fourier. Le schéma simplifié d’un Michelson est le suivant :



La séparatrice est une lame semi réfléchissante permettant la division du faisceau incident en deux faisceaux d’égale intensité. Nous négligerons l’utilité de la compensatrice. Les deux miroirs M1 et M2 sont placés suivant des directions perpendiculaires. Lorsque les distances entre la séparatrice et chacun des miroirs sont égales, chaque rayn lumineux parcours le même chemin optique, la différence de marche est alors nulle et on n’observe pas d’interférence. Lorsqu’on fait varier la distance séparatrice-M1 tout en maintenant la distance séparatrice-M2 constante, on constate l’apparition d’interférences. Observons le schéma suivant :



On note M1 la position du miroir 1 pour laquelle la différence de marche est nulle (c’est le contact optique). On déplace le miroir 1 en M’1. L’image de ce miroir par la compensatrice est M’’1. Le rayon incident (rouge) arrive au niveau de la séparatrice, une partie de ce rayon est réfléchi (rayon vert) en direction du miroir M2 où il s’y réfléchi encore en direction de la lentille. L’autre partie (rayon bleu foncé) est transmise puis se réfléchi sur M’1 retourne sur la séparatrice, s’y réfléchi et redescend vers la lentille. M’’1 étant l’image de M’1 par la séparatrice, le trajet du rayon bleu clair est équivalent à celui du rayon bleu foncé, on se rend alors compte que la différence de marche entre les deux rayons est équivalent à la différence de marche introduite par une lame d’air à face parallèles. On remarque aussi que les rayon émergent du Michelson sont parallèles, ils devraient donc se rencontrer à l’infini, en plaçant une lentille convergente à la sortie du Michelson, on obtiendra une image nette des interférences sur le plan focal objet de la lentille. Différence de marche introduite par une lame à face parallèle Puisque la différence de marche est celle introduite par une lame à face parallèle, il suffit de calculer cette différence de marche.



La différence de marche entre les deux rayons sortant s’écrit:



Et



Donc





Finalement



Interférences avec le Michelson Dans le cas du Michelson, la lame à face parallèle est une lame d’air, de ce fait - i = r - n =1 la différence de marche entre les rayons qui émergent est donc:



L’intensité dans le plan focal de la lentille s’écrit alors :



Et ne dépend que de l’angle d’incidence, c’est pourquoi on appelle ces interférences, interférences d’égales inclinaisons. En sortie du Michelson, l’intensité ne dépend aussi que de l’angle, on observera donc des anneaux d’interférences. On peut montrer que le rayon du kème anneau est donné par :



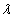Où : - e est l’épaisseur de la lame d’air - f la distance focale de la lentille - la longueur d’onde de la source monochromatique

6. Les fentes d’Young

C’est le dispositif à division de front d’onde le plus courant. Une source ponctuelle S éclaire u écran opaque percé de deux trous. D’après les lois de l’optique géométrique, o s’attend à obtenir l’image de ces deux trous sur l’écran, en réalité, la diffraction intervient si bien qu’on obtient des faisceaux qui se recouvrent. La zone de recouvrement est appelée zone d’interférence.



Les sources S1 et S2 sont des sources cohérentes, de plus ces sources sont éclairées avec la même intensité par S, de ce fait les intensités I1 et I2 de chacune de ce sources sont égales, la formule des interférences se simplifie en :



Où on a noté. Dans la pratique, on observe les interférences sur un écran placé à une distance D>>a. calculons pour un point M de cet écran la différence de marche .



La différence de marche se résume ici à la différence exprimons chacune de ces longueurs. En appliquant la relation de Pythagore :



On peut transformer quelque peu cette expression :



On peut maintenant réaliser un développement limité :



D’où l’expression de la différence de marche :



La différence de marche ne dépend que de x, on obtient donc des franges rectilignes parallèles à l’axe Oy. L’intensité lumineuse sur l’écran s’écrit alors :



On observe des franges sombres, où l’intensité lumineuse est nulle lorsque le cosinus vaut -1 et des franges claires où l’intensité lumineuse est maximale lorsque le cosinus vaut 1. L’espace entre deux franges sombre (ou entre deux franges claires) est appelé interfrange.

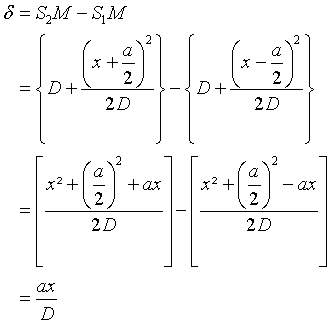
7. Généralités sur la diffraction

Réalisons la petite expérience suivante illustrée par la figure ci-dessous.



Un laser éclaire une fente de largeur a et de hauteur b telle que b>>a. Il est possible de faire varier la largeur de la fente. On constate que lorsque la largeur a est très supérieur à la longueur d’onde du laser, le faisceau n’est pas dévié, il n’y a pas diffraction. En revanche dès que a atteint des dimensions comparables à la longueur d’onde du faisceau il y a éparpillement du faisceau : c’est le phénomène de diffraction. Intéressons nous maintenant à l’intensité diffractée, c‘est à dire à l’intensité lumineuse qui peut être observée sur un écran E placé à une distance D grande devant les dimensions de l’ouverture (loin de l’objet difractant). Dans ces conditions, on dit qu’on étudie la diffraction de Fraunhofer. La première constatation est que la majeure partie de l’intensité correspond à l’image géométrique de la fente. On observe autour de cette image géométrique une succession de frange claie et de frange sombre. Allons un petit peu plus loin dans l’expérience et refermons progressivement la fente. On constate que plus a diminue, plus la figure de diffraction s’étale. L’étalement de la figure de diffraction est inversement proportionnel à la largeur de l’ouverture diffractante. Il est possible de retrouver chacune des constatations précédentes par le calcul en utilisant le principe d’Huygens-Fresnel. Nous n’allons pas faire le détail de calcul, cependant le résultat du calcul est assez simple dans le cas d’une fente rectangulaire. Lorsqu’on éclaire par une onde plane monochromatique une fente rectangulaire et qu’on observe dans un plan très éloigné (idéalement à l’infini) de cette fente l’intensité lumineuse diffractée, celle-ci est donnée par :



Où x désigne l’abscisse du point de l’écran. Cette fonction qu’on appelle un sinus cardinal peut sembler complexe néanmoins la représentation graphique de cette fonction est assez simple.



La largeur du pic central vaut



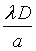La largeur des autres pics de diffraction ne valent que et sont beaucoup moins intense, on vérifie bien, ici, que la majeure partie de l’intensité lumineuse correspond à l’image géométrique. La position des franges sombres est aisément calculable étant donné qu’elles s’obtiennent pour soit . On en déduit finalement que les franges sombres sont obtenues pour :

---

---

---

---

---

---